Answer to Problem 31
Write (4.3) as
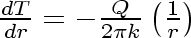
Equation 20
We shall solve for
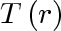 by "separating variables". This technique may be used
only when cross-multiplying enables us to put all
expressions involving one variable (and its
differential) on the left side of the equation and all
expressions involving the other variable (and its
differential) on the right side, as can be done
here. It makes no difference on which sides constants
appear. Multiplying both sides of the equation above
by
by "separating variables". This technique may be used
only when cross-multiplying enables us to put all
expressions involving one variable (and its
differential) on the left side of the equation and all
expressions involving the other variable (and its
differential) on the right side, as can be done
here. It makes no difference on which sides constants
appear. Multiplying both sides of the equation above
by
 , we obtain
, we obtain
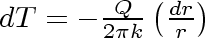
Equation 21
Then from
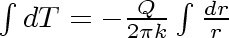
Equation 22
we have

Equation 23
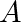 and
and
 arbitrary constants.
arbitrary constants.
Then
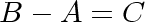 is also an arbitrary constant, and we get
is also an arbitrary constant, and we get
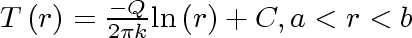
Equation 24
where
 is an arbitrary constant.
is an arbitrary constant.