EX3: Non-Constant Conductivity I
Homework 5.5
Equation (5.6) gives the
temperature distribution in an infinite slab of material of thickness
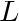 bounded by planes at bounded by planes at  0 and 0 and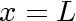 whose temperatures are whose temperatures are 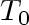 and and
 . Figure 6 shows that the thermal conductivity . Figure 6 shows that the thermal conductivity
 varies with temperature.
varies with temperature.
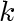 can increase or decrease with
can increase or decrease with
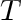 or remain relatively constant.
or remain relatively constant.
The differential equation, (5.2) was solved to obtain the temperature
distribution, equation (5.6).
What we want to do here is to obtain an equation which
represents the solution for every possible specification of
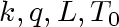 and and
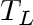 . Note that in this problem . Note that in this problem  is a linear function of
is a linear function of
 . .
Problem
51 - homework!
:
Make equation (5.6)
dimensionless in terms of
 Equation
72
Equation
72
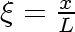 Equation
73
Equation
73
and one dimensionless parameter,
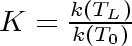 Equation
74
Equation
74
Use equations (5.1)
and (5.3) to represent
 and
and
 . .
Problem
53 - homework!
:
What is your physical interpretation of the parameter
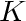 ? ?
| 


