Smale horseshoe and 2D strange repellers
2D Cantor repeller
It is not difficult to get generalized baker's map
if we stretch unit square 3 times, cut it into 3 pieces and put them
one on another. Dynamics of this mapping is equivalent to the Bernoulli
shifts of ternary symbols 0, 1 and 2.
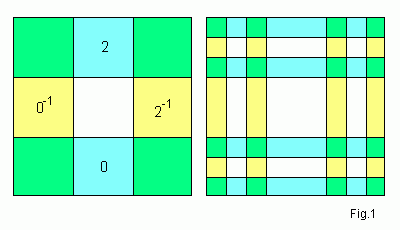 To get 2D Cantor repeller in every iterations we throw away the central
1/3 interval. Under iterations almost all points eventually leave the
square. Remaining invariant set has zero measure.
After the first iteration points of the set are into intersection
of two horizontal strips 0, 2 and two vertical strips
0 -1, 2 -1 (they are preimages of 0, 2).
After the second iteration invariant set is situated into intersection
of the four horizontal (blue) and four vertical (yellow) strips. In the
limit we get 2D Cantor set. Points of the set
have coordinates
To get 2D Cantor repeller in every iterations we throw away the central
1/3 interval. Under iterations almost all points eventually leave the
square. Remaining invariant set has zero measure.
After the first iteration points of the set are into intersection
of two horizontal strips 0, 2 and two vertical strips
0 -1, 2 -1 (they are preimages of 0, 2).
After the second iteration invariant set is situated into intersection
of the four horizontal (blue) and four vertical (yellow) strips. In the
limit we get 2D Cantor set. Points of the set
have coordinates
x = 0. S1 S2 S3 ...
y = 0. S0 S-1 S-2 ... ,
where Sk = 0 or 2. Dynamics on this invariant set
is equivalent to the Bernoulli shifts of the string
... S-2 S-1 S0 ;
S1 S2 ...
Smale horseshoe map
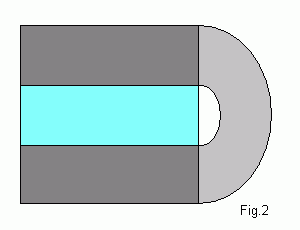 Discontinuous baker's map is not very realistic. But it
turn into continuous Smale horseshoe map if we fold stretched square
as it is shown to the left. It differs from the generalized baker's map
in orientation of the third piece. Its invariant set is again fractal
repeller with zero measure. It has countable set of unstable periodic
cycles and continuum of chaotic orbits.
If a map has horseshoe than it has a region (possibly repelling) with
complex chaotic dynamics.
We meet horseshoe in the Henon map further.
Discontinuous baker's map is not very realistic. But it
turn into continuous Smale horseshoe map if we fold stretched square
as it is shown to the left. It differs from the generalized baker's map
in orientation of the third piece. Its invariant set is again fractal
repeller with zero measure. It has countable set of unstable periodic
cycles and continuum of chaotic orbits.
If a map has horseshoe than it has a region (possibly repelling) with
complex chaotic dynamics.
We meet horseshoe in the Henon map further.
Contents
Previous: Baker's map
Next: The Henon map
updated 29 June 2007
 To get 2D Cantor repeller in every iterations we throw away the central
1/3 interval. Under iterations almost all points eventually leave the
square. Remaining invariant set has zero measure.
After the first iteration points of the set are into intersection
of two horizontal strips 0, 2 and two vertical strips
0 -1, 2 -1 (they are preimages of 0, 2).
After the second iteration invariant set is situated into intersection
of the four horizontal (blue) and four vertical (yellow) strips. In the
limit we get 2D Cantor set. Points of the set
have coordinates
To get 2D Cantor repeller in every iterations we throw away the central
1/3 interval. Under iterations almost all points eventually leave the
square. Remaining invariant set has zero measure.
After the first iteration points of the set are into intersection
of two horizontal strips 0, 2 and two vertical strips
0 -1, 2 -1 (they are preimages of 0, 2).
After the second iteration invariant set is situated into intersection
of the four horizontal (blue) and four vertical (yellow) strips. In the
limit we get 2D Cantor set. Points of the set
have coordinates
 Discontinuous baker's map is not very realistic. But it
turn into continuous Smale horseshoe map if we fold stretched square
as it is shown to the left. It differs from the generalized baker's map
in orientation of the third piece. Its invariant set is again fractal
repeller with zero measure. It has countable set of unstable periodic
cycles and continuum of chaotic orbits.
If a map has horseshoe than it has a region (possibly repelling) with
complex chaotic dynamics.
We meet horseshoe in the Henon map further.
Discontinuous baker's map is not very realistic. But it
turn into continuous Smale horseshoe map if we fold stretched square
as it is shown to the left. It differs from the generalized baker's map
in orientation of the third piece. Its invariant set is again fractal
repeller with zero measure. It has countable set of unstable periodic
cycles and continuum of chaotic orbits.
If a map has horseshoe than it has a region (possibly repelling) with
complex chaotic dynamics.
We meet horseshoe in the Henon map further.