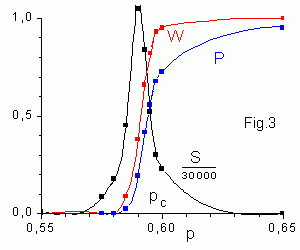
W(p) is the probabilities of appearance of spanning cluster.
P(p) is the probability that an occupied site belongs to the spanning cluster
P(p) = (number of sites in the spanning cluster) / (total number of occudied sites)
The quantity discribes the "density" of the spanning cluster. Because sns is the part of occupied sites in clusters of size s, then the mean cluster size S(p) is
S(p) = ∑s s2ns / ∑s sns = ∑i si2 / ∑i si ,

