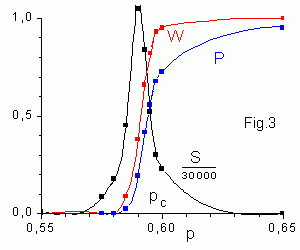
On an infinite lattice there is a type of phase transition from a state with finite isolated clusters to a state with one infinite spanning cluster. The critical point pc marks a singularity, i.e. smooth functions behave singularly at this point (as the size of the lattice tends to infinity). The P(p) behaviour near the critical point is similar to the dependance of order parameter of thermodinamic phase transition (e.g. spontaneous magnetization in ferromagnetic materials).