The Recognition of the Fourth Dimension
By Charles H. Hinton
[This selection is reprinted in its entirely from Bulletin of the Philosophical Society of Washington, Vol 14 (1902). Copy-text: pp 142-162, Speculations on the Fourth Dimension, Selected Writings of Charles H. Hinton, Copyright 1980 by Dover Publications, Inc., ISBN 0-486-23916-0, LC 79-54399.]
THERE are two directions of inquiry in which the research for the physical reality of a fourth dimension can be prosecuted. One is the investigation of the infinitely great, the other is the investigation of the infinitely small.
By the measurement of the angles of vast triangles whose sides are the distances between the stars, astronomers have sought to determine if there is any deviation from the values given by geometrical deduction. If the angles of a celestial triangle do not together equal two right angles, there would be an evidence for the physical reality of a fourth dimension.
This conclusion deserves a word of explanation. If space is really four dimensional, certain conclusions follow which must be brought clearly into evidence if we are to frame the questions definitely which we put to Nature. If space is four dimensional, there must be a solid material sheet against which we move. This sheet must stretch alongside every object in every direction in which it visibly moves. Every material body must slip or slide along this sheet, not deviating from contact with it in any motion which we can observe.
The necessity for this assumption is clearly apparent if we consider the analogous case of a suppositionary plane world. If there were any creatures whose experience were confined to a plane, we must account for their limitation. If they were free to move in every space direction they would have a three-dimensional motion; hence they must be physically limited, and the only way in which we can conceive such a limitation to exist is by means of a material surface against which they slide. The existence of this surface could only be known to them indirectly. It does not lie in any direction from them in which the kinds of motion they know of leads them. If it were perfectly smooth and always in contact with every material object, there would be no difference in their relations to it which would direct their attention to it.
But if this surface were curved--if it were, say, in the form of a vast sphere--the triangles they drew would really be triangles of a sphere, and when these triangles are large enough the angles diverge from the magnitudes they would have for the same lengths of sides if the surface were plane. Hence by the measurement of triangles of very great magnitude, a plane being might detect a difference from the laws of a plane world in his physical world, and so be led to the conclusion that there was in reality another dimension to space a third dimension as well as the two which his ordinary experience made him familiar with.
Now, astronomers have thought it worthwhile to examine the measurements of vast triangles drawn from one celestial body to another with a view to determine if there is anything like a curvature in our space--that is to say, they have tried astronomical measurements to find out if the vast solid sheet against which, on the supposition of a fourth dimension, everything slides is curved or not. These results have been negative. The solid sheet, if it exists, is not curved or, being curved, has not a sufficient curvature to cause any observable deviation from the theoretical value of the angles calculated.
Hence the examination of the infinitely great leads to no decisive criterion. It neither proves nor disproves the existence of a fourth dimension.
Coming now to the prosecution of the inquiry in the direction of the infinitely small, we have to state the question thus: Our laws of movement are derived from the examination of bodies which move in three-dimensional space. All our conceptions are founded on the supposition of a space which is represented analytically by three independent axes and variations along them--that is, it is a space in which there are three independent movements. Any motion possible in it can be compounded out of these three movements, which we may call: up, right, away.
To examine the actions of the very small portions of matter with the view of ascertaining if there is any evidence in the phenomena for the supposition of a fourth dimension of space, we must commence by clearly defining what the laws of mechanics would be on the supposition of a fourth dimension. It is no use asking if the phenomena of the smallest particles of matter are like--we do not know what. We must have a definite conception of what the laws of motion would be on the supposition of the fourth dimension, and then inquire if the phenomena of the activity of the smaller particles of matter resemble the conceptions which we have elaborated.
Now, the task of forming these conceptions is by no means one to be lightly dismissed. Movement in space has many features which differ entirely from movement on a plane; and when we set about to form the conception of motion in four dimensions, we find that there is at least as great a step as from the plane to three-dimensional space.
I do not say that the step is difficult, but I want to point out that it must be taken. When we have formed the conception of four-dimensional motion, we can ask a rational question of Nature. Before we have elaborated our conceptions we are asking if an unknown is like an unknown--a futile inquiry.
As a matter of fact, four-dimensional movements are in every way simple and more easy to calculate than three-dimensional movements, for four-dimensional movements are simply two sets of plane movements put together. It appears to me one of the most marvelous characteristics of the power of the intellect to find how, without any of the familiarity derived from experience, it is possible to grasp the facts of four-dimensional movement and apprehend the consequences of these conceptions.
Without the formation of an experience of four-dimensional bodies, their shapes and motions, the subject can be but formal--logically conclusive, not intuitively evident. It is to this logical apprehension that I must appeal.
It is perfectly simple to form an experiential familiarity with the facts of four-dimensional movement. The method is analogous to that which a plane being would have to adopt to form an experiential familiarity with three-dimensional movements, and may be briefly summed up as the formation of a compound sense by means of which duration is regarded as equivalent to extension.
Consider a being confined to a plane. A square enclosed by four lines will be to him a solid, the interior of which can only be examined by breaking through the lines. If such a square were to pass transverse to his plane, it would immediately disappear. It would vanish, going in no direction to which he could point.
If, now, a cube be placed in contact with his plane, its surface of y contact would appear like the square which we have just mentioned. But if it were to pass transverse to his plane, breaking through it, it would appear as a lasting square. The three-dimensional matter will give a lasting appearance in circumstances under which two-dimensional matter will at once disappear.
Similarly, a four-dimensional cube, or, as we may call it, a tesseract, which is generated from a cube by a movement of every part of the cube in a fourth direction at right angles to each of the three visible directions in the cube, if it moved transverse to our space, would appear as a lasting cube.
A cube of three-dimensional matter, since it extends to no distance at all in the fourth dimension, could instantly disappear if subjected to a motion transverse to our space. It would disappear and be gone without it being possible to point to any direction in which it had moved. All attempts to visualize a fourth dimension are futile. If must be 18 connected with a time experience in three space.
The most difficult notion for a plane being to acquire would be that of rotation about a line. Consider a plane being facing a square: If he were told that rotation about a line were possible, he would move his square this way and that. A square in a plane can rotate about a point, but to rotate about a line would seem to the plane being perfectly impossible. How could those parts of his square which were on one side of an edge come to the other side without the edge moving? He could understand their reflection in the edge. He could form an idea of the looking-glass image of his square lying on the opposite side of the line of an edge, but by no motion that he knows of can he make the actual square assume that position. The result of the rotation would be like reflection in the edge, but it would be a physical impossibility to produce it in the plane.
The demonstration of rotation about a line must be to him purely formal. If he conceived the notion of a cube stretching out in an unknown direction away from his plane, then he can see the base of it, his square in the plane, rotating round a point. He can likewise apprehend that every parallel section taken at successive intervals in the unknown direction rotates in like manner round a point. Thus he would come to conclude that the whole body rotates round a line--the line consisting of the succession of points round which the plane sections rotate. Thus, given three axes, x, y, z; if x rotates to take the place of y, and y turns so as to point to negative x -- then the third axis remaining unaffected by this turning is the axis about which the rotation takes place. This, then, would have to be his criterion of the axis of a rotation--that which remains unchanged when a rotation of every plane section of a body takes place.
There is another way in which a plane being can think about three-dimensional movements; and, as it affords the type by which we can most conveniently think about four-dimensional movements, it will be no loss of time to consider it in detail.
We can represent the plane being and his object by figures cut out of paper, which slip on a smooth surface. The thickness of these bodies must be taken as so minute that their extension in the third dimension escapes the observation of the plane being, and he thinks about them as if they were mathematical plane figures in a plane instead of being material bodies capable of moving on a plane surface. Let Ax, Ay be two axes and ABCD a square (fig. 45). As far as movements in the plane are concerned, the square can rotate about a point, A, for example. It cannot rotate about a side such as AC.
But if the plane being is aware of the existence of a third dimension he can study the movements possible in the ample space, taking his figure portion by portion.
His plane can only hold two axes. But, since it can hold two, he is able to represent a turning into the third dimension if he neglect one of his axes and represent the third axis as lying in his plane. He can make a drawing in his plane of what stands up perpendicularly from his plane. Let Az be the axis, which stands perpendicular to his plane at A. He can draw in his plane two lines to represent the two axes, Ax and Az. Let figure 46 be this drawing. Here the z axis has taken the place of the y axis, and the plane of A x A z is represented in his plane. In this figure all that exists of the square ABCD will be the line AB.
The square extends from this line in the V direction, but more of that direction is represented in figure 46. The plane being can study the turning of the line AB in this diagram. It is simply a case of plane turning around the point A. The line AB occupies intermediate portions like AB' and after half a revolution will lie on Ax produced through A.
Now, in the same way, the plane being can take another point, A', and another line, A'B", in his square. He can make the drawing of the two directions at A', one along A'B", the other perpendicular to his plane. He will obtain a figure precisely similar to figure 46, and will see that, as AB can turn around A, so A'B" around A'.
In this turning AB and A'B" would not interface with each other, as they would if they moved in the plane around the separate points A and A'.
Hence the plane being would conclude that a rotation round a line was possible. He could see his square as it began to make this turning. He could see it half way round when it came to lie on the opposite side of the line AC. But in intermediate portions he could not see it, for it runs out of the plane.
Coming now to the question of a four-dimensional body, let us conceive of it as a series of cubic sections, the first in our space, the rest at intervals, stretching away from our space in the unknown direction.
We must not think of a four-dimensional body as formed by moving a three-dimensional body in any direction which we can see.

Refer for a moment to figure 47. The point A, moving to the right, traces out the line AC. The line AC, moving away in a new direction, traces out the square ACEG at the base of the cube. The square AEGC, moving in a new direction, will trace out the cube ACEGBDHF. The vertical direction of this last motion is not identical with any motion possible in the plane of the base of the cube. It is an entirely new direction, at right angles to every line that can be drawn in the base. To trace out a tesseract the cube must move in a new direction--a direction at right angles to any and every line that can be drawn in the space of the cube.
The cubic sections of the tesseract are related to the cube we see, as the square sections of the cube are related to the square of its base which a plane being sees.
Let us imagine the cube in our space, which is the base of a tesseract, to turn about one of its edges. The rotation will carry the whole body with it, and each of the cubic sections will rotate. The axis we see in our space will remain unchanged, and likewise the series of axes parallel to it, about which each of the parallel cubic sections rotates. The assemblage of all of these is a plane.
Hence in four dimensions a body rotates about a plane. There is no such thing as rotation round an axis.
We may regard the rotation from a different point of view. Consider four independent axes each at right angles to all the others, drawn in a four-dimensional body. Of these four axes we can see any three. The fourth extends normal to our space.
Rotation is the turning of one axis into a second, and the second turning to take the place of the negative of the first. It involves two axes. Thus, in this rotation of a four-dimensional body, two axes change and two remain at rest. Four-dimensional rotation is therefore a turning about a plane.
As in the case of a plane being the result of rotation about a line could appear as the production of a looking-glass image of the original object on the other side of the line, so to us the result of a four-dimensional rotation would appear like the production of a looking-glass image of a body on the other side of a plane. The plane would be the axis of the rotation, and the path of the body between its two appearances would be unimaginable in three-dimensional space.
Let us now apply the method by which a plane being could examine the nature of rotation about a line in our examination of rotation about a plane. Figure 47 represents a cube in our space, the three axes x, y, z, denoting its three dimensions. Let w represent the fourth dimension. Now, since in our space we can represent any three dimensions, we can, if we choose, make a representation of what is in the space determined by three axes x, z, w. This is a three-dimensional space determined by two of the axes we have drawn, x and z, and in place of y the fourth axis, w. We cannot, keeping x and z, have both V and w in our space; so we will let y go and draw w in its place. What will be our view of the cube?
Evidently we shall have simply the square that is in the plane of xz, the square ACDB. The rest of the cube stretches in the y direction, and, as we have none of the space so determined, we have only the face of the cube. This a represented in figure 48.
Now, suppose the whole cube to be turned from the x to the w direction. Conformably with our method, we will not take the whole of the cube into consideration at once, but will begin with the face ABCD.

Let this face begin to turn. Figure 49 represents one of the positions it will occupy; the line AB remains on the z axis. The rest of the face extends between the x and the w direction.
Now, since we can take any three axes, let us look at what lies in the space of zyw, and examine the turning there. We must now let the z axis disappear and let the w axis run in the direction in which z ran.
Making this representation, what do we see of the cube? Obviously we see only the lower face. The rest of the cube lies in the space of xyz. In the space of xyw we have merely the base of the cube lying in the plane of xy, as shown in figure 50.
Now let the x to w turning take place. The square ACEG will turn about the line AE (fig. 51). This edge will remain along they axis and will be stationary, however far the square turns.
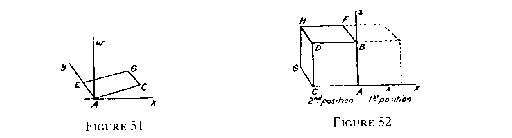
Thus, if the tube be turned by an x to w turning, both the edge AB and the edge AC remain stationary; hence the whole face ABEF in the yz plane remains fixed. The turning has taken place about the face ABEF.
Suppose this turning to continue till AC runs to the left from A. The cube will occupy the position shown in figure 52. This is the looking-glass image of the cube in figure 47. By no rotation in three-dimensional space can the cube be brought from the position in figure 47 to that shown in figure 52.
We can think of this turning as a turning of the face ABCD about AB, and a turning of each section parallel to ABCD round the vertical line in which it intersects the face ABEF, the space in which the turning takes place being a different one from that in which the cube lies.
One of the conditions, then, of our inquiry in the direction of the infinitely small is that we form the conception of a rotation about a plane. The production of a body in a state in which it presents the appearance of a looking-glass image of its former state is the criterion for a four-dimensional rotation.
There is some evidence for the occurrence of such transformations of bodies in the change of bodies from those which produce a right-handed polarization of light to those which produce a left-handed polarization; but this is not a point to which any very great importance can be attached.
Still, in this connection, let me quote a remark from Prof. John G. MeKendrick's address on physiology before the British Association at Glasgow. Discussing the possibility of the hereditary production of characteristics through the material structure of the ovum, he estimates that in it there exist 12,000,000,000 biophors, or ultimate particles of living matter, a sufficient number to account for hereditary transmission, and observes: "Thus it is conceivable that vital activities may also be determined by the kind of motion that takes place in the molecules of that which we speak of as living matter. It may be different in kind from some of the motions known to physicists, and it is conceivable that life may be the transmission to dead matter, the molecules of which have already a special kind of motion of a form of motion sui generis.
Now, in the realm of organic beings symmetrical structures--those with a right and left symmetry--are everywhere in evidence. Granted that four dimensions exist, the simplest turning produces the mirror-image form, and by a folding over, structures could be produced, duplicated right and left, just as in the case of a plane. A symmetrical and lifelike contour is created by the child's amusement of folding an ink-spattered paper along the line of blots.
Whether four-dimensional motions correspond to the physiologist's demand for a special kind of motion or not, I do not know. Our business is with the evidence for its existence in physics. For this purpose it is necessary to examine into the significance of rotation round a plane in the case of extensible and of fluid matter.
Let us dwell a moment longer on the rotation of a rigid body. Looking at the cube in figure 47, which turns about the face of ABFE, we see that any line in the face can take the place of the vertical and horizontal lines we have examined. Take the diagonal line AF and the section through it to GH. The portions of matter which were on one side of AF in this section in figure 47 are on the opposite side of it in figure 52. They have gone round the line AF. Thus the rotation round a face can be considered as a number of rotations of sections round parallel lines in it.
The turning about two different lines is impossible in three-dimensional space. To take another illustration (fig. 53), suppose A and B are two parallel lines in the xy plane, and let CD and EF be two rods crossing them. Now, in the space of xcz if the rods turn round the lines A and B in the same direction they will make two independent circles.
When the end F is going down the end C will be coming up. They will meet and conflict.
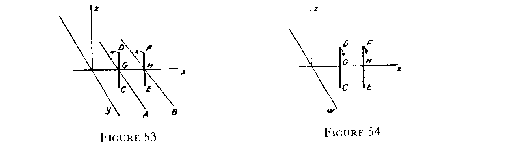
But if we rotate the rods about the plane of AB by the z to w rotation (fig. 54), these movements will not conflict. Suppose all the figure removed with the exception of the plane xz, and from this plane draw the axis of w, so that we are looking at the space of xzw.
Here, figure 54, we cannot see the lines A and B. We see the points G and H, in which A and B intercept the x axis, but we cannot see the lines themselves, for they run in the y direction, and that is not in our drawing.
Now, if the rods move with the z to w rotation, they will turn in parallel planes, keeping their relative positions. The point D, for instance, will describe a circle. At one time it will be above the line A at another time below it. Hence it rotates round A.
Now only two rods, but any number of rods crossing the plane will move round it harmoniously. We can think of this rotation by supposing the rods standing up from one line to move round that line and remembering that it is not inconsistent with this rotation for the rods standing up along another line also to move round it, the relative positions of all the rods being preserved. Now, if the rods are thick together, they may represent a disk of matter, and we see that a disk of matter can rotate round a central plane.
Rotation round a plane is exactly analogous to rotation round an axis in three dimensions. If we want a rod to turn round, the ends must be free; so if we want a disk of matter to turn round its central plane by a four-dimensional turning, all the contour must be free. The whole contour corresponds to the ends of the rod. Each point of the contour can be looked on as the extremity of an axis in the body, round each point of which there is a rotation of the matter in the disk.
If the one end of a rod be clamped, we can twist the rod, but not turn it round; so if any part of the contour of a disk is clamped we can impart a twist to the disk, but not turn it round its central plane. In the case of extensible materials a long, thin rod will twist round its axis, even when the axis is curved; as, for instance, in the case of a ring of India rubber.
In an analogous manner, in four dimensions we can have rotation round a curved plane, if I may use the expression. A sphere can be turned inside out in four dimensions.
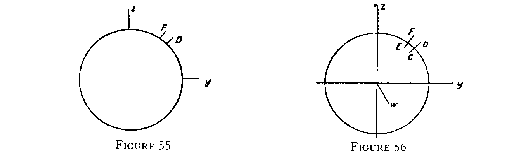
Let figure 55 represent a spherical surface on each side of which a layer of matter exists. The thickness of the matter is represented by the rods CD and EF, extending equally without and within.
Now, take the section of the sphere by the yz plane; we have a circle figure 56. Now, let the w axis be drawn in place of the x axis so that we have the space of yzw represented. In this space all that there will be seen of the sphere is the circle drawn.
Here we see that there is no obstacle to prevent the rods turning round. If the matter is so elastic that it will give enough for the particles at E and C to be separated as they are at F and D, they can rotate round to the position D and F, and a similar motion is possible for all other particles. There is no matter or obstacle to prevent them from moving out in the w direction, and then on round the circumference as an axis. Now, what will hold for one section will hold for all, as the fourth dimension is at right angles to all the sections which can be made of the sphere.
We have supposed the matter of which the sphere is composed to be three dimensional. If the matter had a small thickness in the fourth dimension, there would be a slight thickness in figure 56 above the plane of the paper a thickness equal to the thickness of the matter in the fourth dimension. The rods would have to be replaced by thin slabs. But this would make no difference as to the possibility of the rotation. This motion is discussed by Newcomb in the first volume of the American Journal of Mathematics.
Let us now consider, not a merely extensible body, but a liquid one. A mass of rotating liquid, a whirl, eddy, or vortex, has many remarkable properties. On first consideration we should expect a rotating mass of liquid immediately to spread off and lose itself in the surrounding liquid. The water flies off a wheel whirled round, and we should expect the rotating liquid to be dispersed. But we see the eddies in a river strangely persistent. The rings that occur in puffs of smoke and last so long are whirls or vortices curved round so that their opposite ends join together. A cyclone will travel over great distances.
Helmholtz was the first to investigate the properties of vortices. He studied them as they would occur in a perfect fluid--that is, one without friction of one moving portion or another. In such a medium vortices would be indestructible. They would go on forever, altering their shape, but consisting always of the same portion of the fluid. But a straight vortex could not exist surrounded entirely by the fluid. The ends of a vortex must reach to some boundary inside or outside the fluid.
A vortex which is bent round so that its opposite ends join is capable of existing, but no vortex has a free end in the fluid. The fluid round a vortex is always in motion, and one produces a definite movement in another.
Lord Kelvin has proposed the hypothesis that portions of a fluid segregated in vortices account for the origin of matter. The properties of the aether in respect of its capacity of propagating disturbances can be explained by the assumption of vortices in it instead of by a property of rigidity. It is difficult to conceive, however, of any arrangement of the vortex rings and endless vortex filaments in the aether.
Now, the further consideration of four-dimensional rotations shows the existence of a kind of vortex which would make an aether filled with a homogeneous vortex motion easily thinkable.
To understand the nature of this vortex, we must go on and take a step by which we accept the full significance of the four-dimensional hypothesis. Granted four-dimensional axes, we have seen that a rotation of one into another leaves two unaltered, and these two form the axial plane about which the rotation takes place. But what about these two? Do they necessarily remain motionless? There is nothing to prevent a rotation of these two, one into the other, taking place concurrently with the first rotation. This possibility of a double rotation deserves the most careful attention, for it is the kind of movement which is distinctively typical of four dimensions.
Rotation round a plane is analogous to rotation round an axis. But in three-dimensional space there is no motion analogous to the double rotation, in which, while axis 1 changes into axis 2, axis 3 changes into axis 4.
Consider a four-dimensional body, with four independent axes, x,y,z,w. A point in it can move in only one direction at a given moment. If the body has a velocity of rotation by which the x axis changes into the y axis and all parallel sections move in a similar manner, then the point will describe a circle. If, now, in addition to the rotation by which the x axis changes into they axis the body has a rotation by which the z axis turns into the w axis, the point in question will have a double motion in consequence of the two turnings. The motions will compound, and the point will describe a circle, but not the same circle which it would describe in virtue of either rotation separately.
We know that if a body in three-dimensional space is given two movements of rotation, they will combine into a single movement of rotation round a definite axis. It is in no different condition from that in which it is subjected to one movement of rotation. The direction of the axis changes; that is all. The same is not true about a four-dimensional body. The two rotations x to y and z to w are independent. A body subject to the two is in a totally different condition to that which it is in when subject to one only. When subject to a rotation such as that of x to y, a whole plane in the body, as we have seen, is stationary. When subject to the double rotation no part of the body is stationary except the point common to the two planes of rotation.
If the two rotations are equal in velocity, every point in the body describes a circle. All points equally distant from the stationary point describe circles of equal size.
We can represent a four-dimensional sphere by means of two diagrams, in one of which we take the three axes x, y, and z; in the other the axes x,w, and z. In figure 57 we have the view of a four-dimensional sphere in the space of xyz. Figure 57 shows all that we can see of the four sphere in the space of xyz, for it represents all the points in that space, which are at an equal distance from the center.
Let us now take the xz section, and let the axis of w take the place of the y axis. Here, in figure 58, we have the space of xzw. In this space we have to take all the points which are at the same distance from the center, consequently we have another sphere. If we had a three-dimensional sphere, as has been shown before, we should have merely a circle in the xzw space, the xz circle seen in the space of xzw. But now, taking the view in the space of xzw, we have a sphere in that space also. In a similar manner, whichever set of three axes we take, we obtain a sphere.
In figure 57, let us imagine the rotation in the direction xy to be taking place. The point x will turn to y, and p to p'. The axis remains stationary, and this axis is all of the plane zw which we can see in the space section exhibited in the figure.
In figure 58, imagine the rotation from z to w to be taking place. The w axis now occupies the position previously occupied by the y axis. This does not mean that the w axis can coincide with the y axis. It indicates that we are looking at the four-dimensional sphere from a different point of view. Any three-space view will show us three axes, and in figure 58 we are looking at xzw.
The only part that is identical in the two diagrams is the circle of the x and z axes, which axes are contained in both diagrams. Thus the plane z, x, z' is the same in both, and the point p represents the same point in both diagrams. Now, in figure 58 let the zw rotation take place, the z axis will turn toward the point w of the w axis, and the point p will move in a circle about the point x.

Thus in figure 57 the point p moves in a circle parallel to the xy plane; in figure 58 it moves in a circle parallel to the zw plane, indicated by the arrow.
Now, suppose both of these independent rotations compounded; the point p will move in a circle, but this circle will coincide with neither of the circles in which either one of the rotations will take it. The circle the point p will move in will depend on its position on the surface of the four sphere.
In this double rotation, possible in four-dimensional space, there is a kind of movement totally unlike any with which we are familiar in three-dimensional space. It is a requisite preliminary to the discussion of the behavior of the small particles of matter, with a view to determining whether they show the characteristics of four-dimensional movements, to become familiar with the main characteristics of this double rotation. And here I must rely on a formal and logical assent rather than on the intuitive apprehension which can only be obtained by a more detailed study.
In the first place this double rotation consists in two varieties or kinds, which we will call the A and B kinds. Consider four axes, x, y, z, a'. The rotation of x to y can be accompanied with the rotation of z to w. Call this the A kind.
But also the rotation of x to y can be accompanied by the rotation of not z to w, but w to z. Call this the B kind.
They differ in only one of the component rotations. One is not the negative of the other. It is the semi-negative. The opposite of an x to y, z to w rotation would be y to x, w to z. The semi-negative is x to y and w to z.
If four dimensions exist and we cannot perceive them because the extension of matter is so small in the fourth dimension that all movements are withheld from direct observation except those which are three dimensional, we should not observe these double rotations, but only the effects of them in three-dimensional movements of the type with which we are familiar.
If matter in its small particles is four dimensional we should expect this double rotation to be a universal characteristic of the atoms and molecules, for no portion of matter is at rest. The consequences of this corpuscular motion can be perceived, but only under the form of ordinary rotation or displacement. Thus if the theory of four dimensions is true we have in the corpuscles of matter a whole world of movement which we can never study directly, but only by means of inference.
The rotation A, as I have defined it, consists of two equal rotations--one about the plane of zw, the other about the plane of xy. It is evident that these rotations are not necessarily equal. A body may be moving with a double rotation in which these two independent components are not equal; but in such a case we can consider the body to be moving with a composite rotation--a rotation of the A or B kind and, in addition, a rotation about a plane.
If we combine an A and a B movement, we obtain a rotation about a plane; for, the first being x to y and z to w, and the second being x to y and w to z, when they are put together the z to w and w to z rotations neutralize each other, and we obtain an x to y rotation only, which is a rotation about the plane of zw. Similarly. if we take a B rotation, y to x and z to w, we get, on combining this with the A rotation, a rotation of z to w about the xy plane. In this case the plane of rotation is in the three-dimensional space of xyz, and we have--what has been described before--a twisting about a plane in our space.
Consider now a portion of a perfect liquid having an A motion. It can be proven that it possesses the properties of a vortex. It forms a permanent individuality--a separated-out portion of the liquid--accompanied by a motion of the surrounding liquid. It has properties analogous to those of a vortex filament. But it is not necessary for its existence that its ends should reach the boundary of the liquid. It is self-contained and, unless disturbed, is circular in every section.
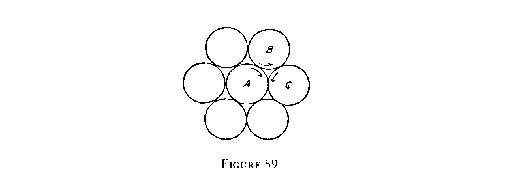
If we suppose the aether to have its properties of transmitting vibration given it by such vortices, we must inquire how they lie together in four-dimensional space. Placing a circular disk on a plane and surrounding it by six others (fig. 59), we find that if the central one is given a motion of rotation, it imparts to the others a rotation which is antagonistic in every two adjacent ones. If A goes round as shown by the arrow, B and C will be moving in opposite ways, and each tends to destroy the motion of the other.
Now, if we suppose spheres to be arranged in a corresponding manner in three-dimensional space, they will be grouped in figures which are for three-dimensional space what hexagons are for plane space. If a number of spheres of soft clay be pressed together, so as to fill up the interstices, each will assume the form of a 14-sided figure, called a tetrakaidecagon.
Now, assuming space to be filled with such tetrakaidecagons and placing a sphere in each, it will be found that one sphere is touched by six others. The remaining eight spheres of the fourteen which surround the central one will not touch it, but will touch three of those in contact with it. Hence if the central sphere rotates it will not necessarily drive those around it so that their motions will be antagonistic to each other, but the velocities will not arrange themselves in a systematic manner.
In four-dimensional space the figure which forms the next term of the series hexagon, tetrakaidecagon, is a thirty-sided figure. It has for its faces ten solid tetrtkaidecagons and twenty hexagonal prisms. Such figures will exactly fill four-dimensional space, five of them meeting at every point. If, now, in each of these figures we suppose a solid four-dimensional sphere to be placed, any one sphere is surrounded by thirty others. Of these it touches ten, and, if it rotates, it drives the rest by the means of these. Now, it we imagine the central sphere to be given an A or a B rotation, it will turn the whole mass of spheres round in a systematic manner. Suppose four-dimensional space to be filled with such spheres, each rotating with a double rotation, the whole mass would form one consistent system of motion, in which each one drove every other one, with no friction or lagging behind.
Every sphere would have the same kind of rotation. In three-dimensional space, if one body drives another round, the second body rotates with the opposite kind of rotation; but in four-dimensional space these four-dimensional spheres would each have the double negative of the rotation of the one next it, and we have seen that the double negative of an A or B rotation is still an A or B rotation. Thus four-dimensional space could be filled with a system of self-preservative living energy. If we imagine the four-dimensional spheres to be of liquid and not of solid matter, then, even if the liquid were not quite perfect and there were a slight retarding effect of one vortex on another, the system would still maintain itself.
In this hypothesis we must look on the aether as possessing energy, and its transmission of vibrations, not as the conveying of a motion imparted from without, but as a modification of its own motion.
We are now in possession of some of the conceptions of four-dimensional mechanics, and will turn aside from the line of their development to inquire if there is any evidence of their applicability to the processes of nature.
Is there any mode of motion in the region of the minute which, giving three-dimensional movements for its effect, still in itself escapes the grasp of our mechanical theories? I would point to electricity. Through the labors of Faraday and Maxwell we are convinced that the phenomena of electricity are of the nature of the stress and strain of a medium; but there is still a gap to be bridged over in their explanation--the laws of elasticity, which Maxwell assumes, are not those of ordinary matter. And, to take another instance: a magnetic pole in the neighborhood of a current tends to move. Maxwell has shown that the pressures on it are analogous to the velocities in a liquid which would exist if a vortex took the place of the electric current; but we cannot point out the definite mechanical explanation of these pressures. There must be some mode of motion of a body or of the medium in virtue of which a body is said to be electrified.
Take the ions which convey charges of electricity 500 times greater in proportion to their mass than are carried by the molecules of hydrogen in electrolysis. In respect of what motion can these ions be said to be electrified? It can be shown that the energy they possess is not energy of rotation. Think of a short rod rotating. If it is turned over it is found to be rotating in the opposite direction. Now, if rotation in one direction corresponds to positive electricity, rotation in the opposite direction corresponds to negative electricity, and the smallest electrified particles would have their charges reversed by being turned over--an absurd supposition.
If we fix on a mode of motion as a definition of electricity, we must have two varieties of it, one for positive and one for negative; and a body possessing the one kind must not become possessed of the other by any change in its position.
All three-dimensional motions are compounded of rotations and translations, and none of them satisfy this first condition for serving as a definition of electricity.
But consider the double rotation of the A and B kinds. A body rotating with the A motion cannot have its motion transformed into the B kind by being turned over in any way. Suppose a body has the rotation x to y and z to w. Turning it about the xy plane, we reverse the direction of the motion x to y. But we also reverse the z to w motion, for the point at the extremity of the positive z axis is now at the extremity of the negative z axis, and since we have not interfered with its motion, it goes in the direction of position w. Hence we have y to x and w to z, which is the same as x to y and z to w. Thus both components are reversed, and there is the A motion over again. The B kind is the semi-negative, with only one component reversed.
Hence a system of molecules with the A motion would not destroy it in one another, and would impart it to a body in contact with them. Thus A and B motions possess the first requisite which must be demanded in any mode of motion representative of electricity.
Let us trace out the consequences of defining positive electricity as an A motion and negative electricity as a B motion. The combination of positive and negative electricity produces a current. Imagine a vortex in the aether of the A kind and unite with this one of the B kind. An A motion and a B motion produce rotation round a plane, which is in the aether a vortex round an axial surface. It is a vortex of the kind we represent as a part of a sphere turning inside out. Now, such a vortex must have its rim on a boundary of the aether--on a body in the aether.
Let us suppose that a conductor is a body which has the property of serving as the terminal abutment of such a vortex. Then the conception we must form of a closed current is of a vortex sheet having its edge along the circuit of the conducting wire. The whole wire will then be like the centers on which a spindle turns in three-dimensional space, and any interruption of the continuity of the wire will produce a tension in place of a continuous revolution.
As the direction of the rotation of the vortex is from a three-space direction into the fourth dimension and back again, there will be no direction of flow to the current; but it will have two sides, according to whether z goes to w or z goes to negative w.
We can draw any line from one part of the circuit to another; then the aether along that line is rotating round its points.
This geometric image corresponds to the definition of an electric circuit. It is known that the action does not lie in the wire, but in the medium, and it is known that there is no direction of flow in the wire.
No explanation has been offered in three-dimensional mechanics of how an action can be impressed throughout a region and yet necessarily run itself out along a closed boundary, as is the case in an electric current. But this phenomenon corresponds exactly to the definition of a four-dimensional vortex.
If we take a very long magnet, so long that one of its poles is practically isolated, and put this pole in the vicinity of an electric circuit, we find that it moves.
Now, assuming for the sake of simplicity that the wire which determines the current is in the form of a circle, if we take a number of small magnets and place them all pointing in the same direction normal to the plane of the circle, so that they fill it and the wire binds them round, we find that this sheet of magnets has the same effect on the magnetic pole that the current has. The sheet of magnets may be curved, but the edge of it must coincide with the wire. The collection of magnets is then equivalent to the vortex sheet and an elementary magnet to a part of it. Thus, we must think of a magnet as conditioning a rotation in the aether round the plane which bisects at right angles the line joining its poles.
If a current is started in a circuit, we must imagine vortices like bowls turning themselves inside out, starting from the contour. In reaching a parallel circuit, if the vortex sheet were interrupted and joined momentarily to the second circuit by a free rim, the axis plane would lie between the two circuits, and a point on the second circuit opposite a point on the first would correspond to a point opposite to it on the first; hence we should expect a current in the opposite direction in the second circuit. Thus the phenomena of induction are not inconsistent with the hypothesis of a vortex about an axial plane.
In four-dimensional space in which all four dimensions were commensurable, the intensity of the action transmitted by the medium would vary inversely as the cube of the distance. Now, the action of a current on a magnetic pole varies inversely as the square of the distance; hence over measurable distances the extension of the aether in the fourth dimension cannot be assumed as other than small in comparison with those distances. This extension being small, the effect of a vortex sheet would be equivalent to a number of jets on one side and suctions on the other.
Such an arrangement in the case of a liquid would produce velocities in the liquid which coincide in direction with the tendency of motion of a magnetic pole. But analogies of this kind leave out of sight the fact that the action is a reciprocal one. Non-magnetic matter shows no tendency to move. To arrive at a definite conclusion it will be necessary to investigate the resultant pressures which accompany the collocation of solid vortices with surface ones.
To recapitulate: The movements and mechanics of four-dimensional space are definite and intelligible. A vortex with a surface as its axis affords a geometric image of a closed circuit, and there are rotations which by their polarity afford a possible definition of statical electricity.