The Degree Sequence of a Graph
Refining technique
This technique is often used to establish that two given
graphs are not isomorphic. Sometimes, the
technique is used to establish
that two graphs are isomorphic; in this case, the technique usually helps
construct an isomorphic mapping between the two graphs.
The refining technique comprises hierarchically arranged statements proving
that some parameters of graphs are their
invariants. An example of such a statement is
Proposition 1, which establishes that a vertex degree is an invariant of
a graph.
The partitioning procedure amplifies this invariant into a set of invariants
that, for some graphs, completely determine the graph.
Procedure Split
Input: graph G(V, E);
Step 1:
|
Partition V into subsets
so that two vertices belong to the same subset
Vi
if they have the same degree.
Let di be the degree of the vertices in
Vi.
|
Step 2:
|
Reorder the partitions so that
.
|
Step 3:
|
Output the partitioning
and the degrees
.
|
|
Example
Proposition 2
Let G and H be isomorphic graphs and let
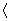 (V1, …, Vk);
(d1 < … < dk)
(V1, …, Vk);
(d1 < … < dk)
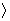 and
and
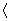 (U1, …, Uk);
(c1 < … < ck)
(U1, …, Uk);
(c1 < … < ck)
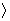 be the outputs of Split(G) and Split(H). Then
be the outputs of Split(G) and Split(H). Then
- k = t, |V1| = |U1|,
…, |Vk| = |UK|, and
- d1 = c1, …,
dk = ck
Copyright
2000
Rensselaer Polytechnic Institute. All Rights Reserved.
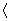 (V1, …, Vk);
(d1 < … < dk)
(V1, …, Vk);
(d1 < … < dk)
 and
and
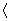 (U1, …, Uk);
(c1 < … < ck)
(U1, …, Uk);
(c1 < … < ck)
 be the outputs of Split(G) and Split(H). Then
be the outputs of Split(G) and Split(H). Then