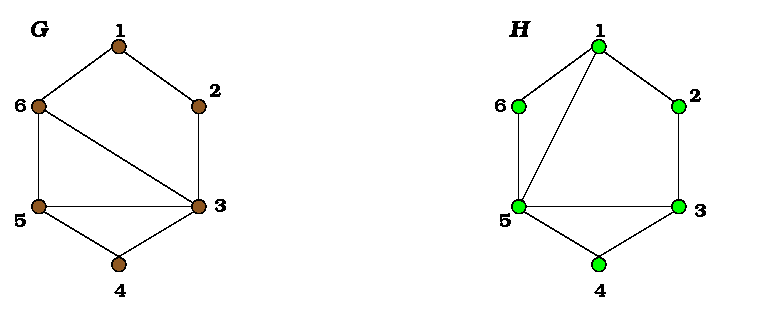
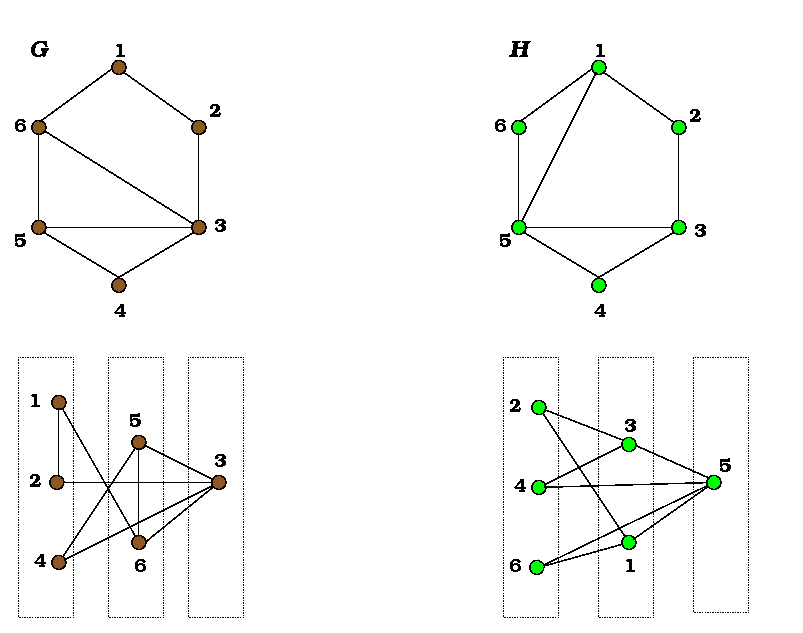
We see that the conclusion of Proposition 2 is satisfied. However, it is clear from the partitionings that the graphs are not isomorphic. One way of seeing this is as follows:
If there were an isomorphic mapping between the graphs, then
U3 = {5} would have to be mapped onto V3
= {3}, and U2 = {1, 3} would have to be mapped onto
V2 = {5, 6}. But no matter how U2 is
mapped onto V2, the vertices of U2 are not
adjacent while the corresponding-to-be vertices of V2
are adjacent. This contradicts the definition of isomorphism, and it
leads us to our next proposition.