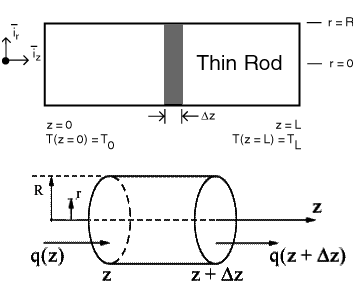
Figure 1
|
|
| (3.1) |
|
To begin the derivation choose an arbitrary value of z, and slice the rod
with planes perpendicular to the axis at positions z and
, where
is assumed small. Now consider the solid circular cylinder shown, of radius
R and thickness
We shall now derive equation (3.1) by formulating the "heat balance", which relates Qgen to the rate at which heat is conducted along the rod.
Let Hgen denote the rate at which heat is generated within the finite cylinder of length previously shown, and let Hb denote the net rate of heat flow outward through the surface of the cylinder. Then under steady state conditions| (3.2) |
|
|
| expresses the heat balance. Now | ||
| (3.3a) |
|
units: Watts |
| while | ||
| (3.3b) |
|
units: Watts |
|
|
||
|
|
||
| so that |
|
|
| From Fourier's law, , we have | ||
|
|
||
| Therefore | ||
| (3.4) |
|
|
| Substituting (3.3a) and (3.4) into (3.2), gives | ||
|
|
||
| Dividing by , and then letting , we get | ||
|
|
||
| and Equation (3.1). | ||
Analysis Link I presents an alternative derivation to equation (3.1) using vector calculus. It gives the derivation of the partial differential equation for heat conduction with sources and sinks located within the region where heat conduction is under study. (Analysis Link I - equation 20). That equation is then simplified to obtain equation (3.1).