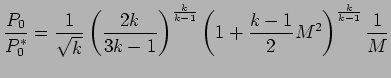Next: 6 Fanno Flow
Up: Free textbook pdf Fundamentals
Previous: 4 Normal Shock
![$\displaystyle {P_{0} \over P_{0}^{*}} = {P \over P^{*}} \left[ {1 + { k -1 \ove...
... ^ {2} \over { 1 + {k -1 \over 2k} } } \right] ^ { k \over k -1 } %\label{eq:}
$](img66.png) |
(55) |
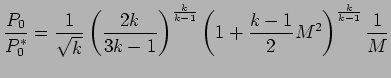 |
(56) |
For the case that
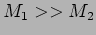 and
and
 equation (58) is
reduced into the following approximation
equation (58) is
reduced into the following approximation



Next: 6 Fanno Flow
Up: Free textbook pdf Fundamentals
Previous: 4 Normal Shock
Genick Bar-Meir ||| www.potto.org
copyright Dec , 2006
The pdf version is also available here
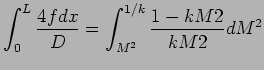
![$\displaystyle {P_{0} \over P_{0}^{*}} = {P \over P^{*}} \left[ {1 + { k -1 \ove...
... ^ {2} \over { 1 + {k -1 \over 2k} } } \right] ^ { k \over k -1 } %\label{eq:}
$](img66.png)