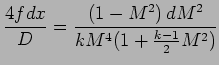Next: 7 RAYLEIGH FLOW
Up: Free textbook pdf Fundamentals
Previous: 5 Isothermal Flow
6 Fanno Flow
A representative friction factor is defined as



Next: 7 RAYLEIGH FLOW
Up: Free textbook pdf Fundamentals
Previous: 5 Isothermal Flow
Genick Bar-Meir ||| www.potto.org
copyright Dec , 2006
The pdf version is also available here