


Next: 8.1 Given Two Angles,
Up: Free textbook pdf Fundamentals
Previous: 7 RAYLEIGH FLOW
8 Oblique-Shock
The Rankine-Hugoniot relations are the same as the
relationship for the normal shock
where
and
and
Where
and where the definition of the 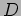 is
is
and where the definitions of 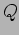 and
and 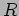 are
are
and
A simplified case of the Maximum Deflection Mach Number's
equation for
large Mach number becomes
The density ratio can be expressed as
The ratio of the total pressure can be expressed as
Subsections



Next: 8.1 Given Two Angles,
Up: Free textbook pdf Fundamentals
Previous: 7 RAYLEIGH FLOW
Genick Bar-Meir ||| www.potto.org
copyright Dec , 2006
The pdf version is also available here
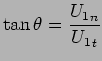
![]() is
is