Отображение Эно
Из необратимого квадратичного отображения можно
построить обратимое двумерное отображение Эно (Henon map)
x' = a + x2 + by,
y' = x.
Легко найти обратное отображение
x = y',
y = (x' - y' 2 - a)/b.
Отображение сжимающее для |b| < 1.
Все ограниченные притягивающие орбиты лежат в этом интервале и
аттрактор обладает нулевой площадью.

Отображение можно представить как последовательность трех простых
операций:
однородного сжатия в b раз в направлении оси y
(слева сжатие опущено, т.е. b = 1)
x' = x, y' = by,
деформации в этом же направлении
x' = x,
y' = a + x2 + y
и отражении относительно диагонали y = x
x' = y, y' = x.
Подкова Смейла
Ниже показано, как отображение Эно f N
переводит квадратную область с вершинами
(±3.9, ±3.9) в покову Смэйла.
После второй итерации получается двойная подкова.
Обратное отображение (при N < 0) переводит квадрат в
вертикальную подкову. Точки инвариантного множества
(которые не уходят на бесконечность и всегда остаются внутри квадрата)
лежат в пересечении двух трансверсальных подков.
При каждой последующей итерации внутри любой области пересечения возникает
четыре новых пересечения (нажмите кнопку "+", чтобы убедиться в этом).
При N → ∞ образуется фрактальный канторов репеллер.
Щелкните мышкой с <Alt>/<Ctrl>, чтобы изменить масштаб
картинки.
Устойчивые и неустойчивые многообразия и гомоклинические структуры
Для гиперболической неподвижной точки можно построить устойчивое
Ws и неустойчивое Wu многообразия,
состоящие изо всех точек, которые при итерациях отображения стремятся к ней
при N → ∞ и -∞ соответственно.
В двумерном случае это седловая точка и две идущие к ней устойчивые и две
выходящие из нее неустойчивые сепаратрисы.
Т.к. любая область неподвижной точки растягивается при итерациях отображения
вдоль неустойчивого многообразия и сжимается в трансверсальном направлении,
то качестенно за неустойчивыми сепаратрисами можно проследить, если наблюдать
за этой эволюцией. Чтобы построить устойчивые сепаратрисы следует итерировать
обратное отображение.
Ниже вы видите результаты N итераций окрестности (радиуса R)
неподвижной точки x1 отображения Эно.
С помощью мышки и квадрата легко убедиться, что устойчивые сепаратрисы
окрашены в синий цвет, а неустойчивые в красный.
Пусть устойчивая и неустойчивая сепаратрисы пересекается в некоторой
гомоклинической точке go . Эта точка лежит на
устойчивом многообразии и ее итерации сходятся к седлу. Т.к. эта орбита
проходит через g1 = f(go ), то эта точка
также лежит на ws . При итерациях обратного отображения
орбита go стремится к седлу вдоль неустойчивого многообразия.
Т.к. g1 = f-1(go ), то при итерациях
обратного отображения она также будет стремиться к x1 .
Т.е. g1 лежит на нейстойчивой сепаратрисе и является
пересечением ws и wu .
Поэтому имеется бесконечное множество пересечений g2 ,
g3 ...
Чтобы сделать это утверждение более строгим, покажем, что присутствие
гомоклинической структуры свидетельствует о наличии у отображения подковы
Смейла.
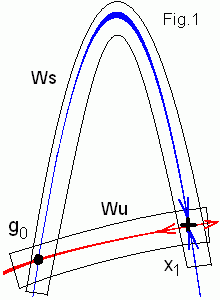 Пусть у отображения есть гомоклиническая точка go .
Выберем некоторую область D вокруг седла. A = f ok(D)
будет растягиваться вдоль неустойчивой сепаратрисы и при некотором
k достигнет гомоклинической точки. Аналогично, область
B = f -om(D) будет растягиваться вдоль устойчивой сепаратрисы
и также достигнет go . Поэтому f -o(k+m)
переводит область A в B и задает отображение подковы, как это
показано на рисунке.
Точки пересечения устойчивых и неустойчивых многообразий двух разных
гиперболических точек называются гетероклиническими. Для них также
строится отображение подковы и фрактальные странные множества.
Пусть у отображения есть гомоклиническая точка go .
Выберем некоторую область D вокруг седла. A = f ok(D)
будет растягиваться вдоль неустойчивой сепаратрисы и при некотором
k достигнет гомоклинической точки. Аналогично, область
B = f -om(D) будет растягиваться вдоль устойчивой сепаратрисы
и также достигнет go . Поэтому f -o(k+m)
переводит область A в B и задает отображение подковы, как это
показано на рисунке.
Точки пересечения устойчивых и неустойчивых многообразий двух разных
гиперболических точек называются гетероклиническими. Для них также
строится отображение подковы и фрактальные странные множества.
Содержание
«Подкова Смейла
»Бифуркационная диаграмма
изменено 25 июня 2007
 Пусть у отображения есть гомоклиническая точка go .
Выберем некоторую область D вокруг седла. A = f ok(D)
будет растягиваться вдоль неустойчивой сепаратрисы и при некотором
k достигнет гомоклинической точки. Аналогично, область
B = f -om(D) будет растягиваться вдоль устойчивой сепаратрисы
и также достигнет go . Поэтому f -o(k+m)
переводит область A в B и задает отображение подковы, как это
показано на рисунке.
Точки пересечения устойчивых и неустойчивых многообразий двух разных
гиперболических точек называются гетероклиническими. Для них также
строится отображение подковы и фрактальные странные множества.
Пусть у отображения есть гомоклиническая точка go .
Выберем некоторую область D вокруг седла. A = f ok(D)
будет растягиваться вдоль неустойчивой сепаратрисы и при некотором
k достигнет гомоклинической точки. Аналогично, область
B = f -om(D) будет растягиваться вдоль устойчивой сепаратрисы
и также достигнет go . Поэтому f -o(k+m)
переводит область A в B и задает отображение подковы, как это
показано на рисунке.
Точки пересечения устойчивых и неустойчивых многообразий двух разных
гиперболических точек называются гетероклиническими. Для них также
строится отображение подковы и фрактальные странные множества.
