Кусочно-линейные отображения
Многие особенности хаотических систем можно продемонстрировать
на примере удивительно простого одномерного отображения.
Отображение "зуб пилы" и сдвиги Бернулли
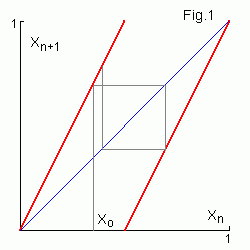 На Fig.1 приведено отображение зуб пилы
На Fig.1 приведено отображение зуб пилы
xn+1 = 2xn (mod 1),
где x (mod 1) означает дробную часть x.
В двоичной системе счисления умножение на 2 соответствует сдвигу всего
числа влево на один разряд, а взятие целой части - отбрасыванию старшего
разряда, поэтому xn+1 получается из
xn сдвигом Бернулли
xo = 0.01011 ...
x1 = 0.1011 ...
x2 = 0.011 ...
Последовательность (xo , x1 ...) называется
орбитой точки xo.
Символическая динамика и хаос
Очевидно, что если в двоичном представлении xo n-ая
первая цифра после точки 0, то xn лежит в левой
половине интервала [0,1], а если 1, то в правой.
Поэтому для отображения пилы орбита может быть однозначно задана
последовательностью посещений (so , s1 ...)
правой или левой половины интервала - символической последовательностью
σ.
Для случайной σ последовательности точки орбиты будут посещать
левую или правую половину интервала случайным образом!
Существование такого континуума сложных траекторий считается одним из
признаков хаоса.
 Можно предположить, что хаос (и перемешивание траекторий) возникает из-за
разрыва отображения зуб пилы при x = 1/2. Однако подобное хаотическое
поведение наблюдается у непрерывного отображения "тент" (см. Fig.2 ниже)
и у совершенно гладкого квадратичного отображения.
Для отображения тент правила перевода символической последовательности
в двоичный код сложнее, чем для отображения пилы (см.
Динамика отображения тент на следующей странице).
Однако, существует простой трюк, позволяющий строить хаотические
последовательности для необратимых отображений.
Как видно из рисунка, при заданом xn всегда можно
выбрать предшествующее значение xn-1 лежащим в левом
или в правом интервале.
Поэтому итерируя обратное отображение легко построить орбиту для любой
символической последовательности (в том числе и хаотической).
Можно предположить, что хаос (и перемешивание траекторий) возникает из-за
разрыва отображения зуб пилы при x = 1/2. Однако подобное хаотическое
поведение наблюдается у непрерывного отображения "тент" (см. Fig.2 ниже)
и у совершенно гладкого квадратичного отображения.
Для отображения тент правила перевода символической последовательности
в двоичный код сложнее, чем для отображения пилы (см.
Динамика отображения тент на следующей странице).
Однако, существует простой трюк, позволяющий строить хаотические
последовательности для необратимых отображений.
Как видно из рисунка, при заданом xn всегда можно
выбрать предшествующее значение xn-1 лежащим в левом
или в правом интервале.
Поэтому итерируя обратное отображение легко построить орбиту для любой
символической последовательности (в том числе и хаотической).
 В общем случае для произвольного отображения разрешены не любые
σ-последовательности. Так для несимметричной пилы (слева) в правый
интервал можно попасть только из левого, поэтому комбинации 11 запрещены.
В общем случае для произвольного отображения разрешены не любые
σ-последовательности. Так для несимметричной пилы (слева) в правый
интервал можно попасть только из левого, поэтому комбинации 11 запрещены.
Отображение пилы позволяет легко продемонстрировать и другие характерные
особенности хаотических систем.
Неустойчивость и показатели Ляпунова
Если у двух близких точек xo и yo равны
первые k двоичных знаков, то для отображения пилы, пока n < k
yn - xn =2 n
(yo - xo ) = (yo - xo )
e n ln 2.
Т.о. расстояние между двумя близкими орбитами экспоненциально расходится
с ростом n. Это свойство называют также чувствительностью к
начальным условиям. Оно означает кроме того, что все периодические орбиты
отображения неустойчивы.
Показатель экспоненты называется показателем Ляпунова и для этого
отображения Λ = ln 2.
После k итераций расстояние между xn и
yn будет порядка 1.
Неустойчивые периодические орбиты
Для отображения пилы известно, что начинающаяся при рациональном x = p/q
орбита периодическая, если q - нечетное. Например, орбита 1/3
имеет период 2
1/3 → 2/3 → 1/3 ... ,
а для 1/7 получается орбита с периодом 3
1/7 → 2/7 → 4/7 → 1/7 ...
При четном q траектория выходит на периодическую орбиту через
несколько итераций, например
1/6 → 1/3 → 2/3 → 1/3 ... или
1/8 → 1/4 → 1/2 → 1 → 1 ...
Т.о. у отображения существует бесконечное (счетное) множество
неустойчивых периодических орбит и они плотны на интервале [0,1].
Если в конце любой конечной двоичной последовательности добавить
периодическую последовательность, соответствующую неустойчивой
периодической орбите, то полученная точка будет прообразом
этой орбиты. Т.к. исходное число можно выбрать как угодно близко
к любой точке [0, 1], то прообразы любой орбиты плотны на
этом интервале.
 Примеры: На Fig.4 показана вторая итерация отображения пилы и две точки
орбиты с периодом 2, полученные из символической последовательности
σ = (01) (см. Приложение)
Примеры: На Fig.4 показана вторая итерация отображения пилы и две точки
орбиты с периодом 2, полученные из символической последовательности
σ = (01) (см. Приложение)
x0 = 0.0101... = 0.(01) = 1 / 112
= 1/3,
x1 = 0.1010... = 0.(10) =
102 / 112 = 2/3
Две последние комбинации x2 = 0.(00) = 0 и
x3 = 0.(11) = 1 неподвижные точки отображения (с периодом 1).
Приведем также две орбиты с периодом 3
x0 = 0.001001... = 0.(001) =
12 / 1112 = 1/7,
x1 = 0.(010) = 2/7,
x2 = 0.(100) = 4/7
и x3 = 0.(110) = 6/7,
x4 = 0.(101) = 5/7,
x5 = 0.(011) = 3/7.
Растягивание, складывание и необратимость
Преобразование пилы состоит из равномерного растягивания исходного отрезка
в 2 раза и сдвига его правой половины на -1. Очевидно, что растяжение
ведет к экспоненциальной расходимости близлежащих точек. Сдвиг сохраняет
ограниченность области отображения, но приводит также к его необратимости,
т.к. две различные точки xn отображаются в одну
xn+1.
Необратимость следует также из отбрасывания старшего символа
последовательности при сдвиге Бернулли.
Shadowing
Экспоненциальный рост ошибок округления в хаотической системе означает,
что компьютерная псевдо-траектория быстро уходит от
точной орбиты. Однако для данного xn псевдо-траектории
мы можем построить траекторию итерируя обратное отображение. Т.к. обратное
отображение - сжимающее, то обратные итерации устойчивы и обратная траектория
останется близкой к точной. Существование такой точной траектории, близкой
к псевдо-траектории называется shadowing. Благодаря этому явлению, мы
можем доверять результатам рассчетов на ПК.
Инвариантное распределение и мера
В физическом и компьютерном эксперименте мы можем задать начальные
условия только приближенно. Но для любой конечной точности данных
хаотическая динамика предсказуема только до конечного числа итераций!
Для такого "турбулентного" процесса статистическое описание кажется более
подходящим, чем знание точных орбит. Для этого следует следить за
эволюцией (плотности) распределений точек.
После каждой итерации отображения пилы расстояние между близлежащими
точками удваивается, поэтому гладкое распределение также расплывается в два
раза. Т.к. все точки лежат в ограниченном интервале [0,1], то
в пределе n → ∞ мы получим однородное распределение
точек ρ(x)=1. Отображение не меняет этого распределения и оно
называется стационарным или инвариантным распределением
(заметим, что точки неустойчивых переодических орбит образуют сингулярные
инвариантные распределения).
Эргодичность
Выберем случайную орбиту
xo = 0.a1a2a3...
тогда для любого числа
s = 0.b1b2b3...bk
мы всегда можем найти где то в xo совпадающую
подпоследовательность, т.е. xn пройдет близко к s
(и вероятность этого прохождения не зависит от s). Поэтому
случайная орбита пройдет сколь угодно близко к любой точке интервала
[0,1] и покроет его равномерно в соответствии с однородной
инвариантной плотностью.
Мы можем использовать это для замены при n → ∞
средних по "времени" средними по "ансамблю" (эргодичность)
<A> = ∑n
A(xn) = ∫ A(x) dx.
В общем случае для хаотического отображения
<A> = ∑n A(xn) =
∫ A(x) dμ = ∫ A(x) ρ(x) dx ,
где μ - инвариантная мера, а
ρ(x) - инвариантная плотность отображения.
Вырожденное отображение окружности
Вырожденное отображение окружности
xn = xn-1+Δ
(mod 1) = xo+ nΔ (mod 1)
регулярно "наматывает" точки xn на интервал [0,1]
(если соединить концы интервала 0 и 1 то образуется окружность).
Для рационального Δ = p/q все орбиты периодичны с периодом
q. Для иррационального Δ каждая орбита равномерно
и плотно покрывает интервал [0,1], поэтому для этого отображения
также можно ввести инвариантное распределение для вычисления средних.
Отметим, однако, что все точки на окружности [0,1] смещаются
отображением на одно и то же Δ. Поэотму расстояние между орбитами
остается постоянным и любое распределение точек сохраняет
свою форму. Т.е. мы получили инвариантное распределение без перемешивания.
Перемешивание и затухание корреляций
Корреляционная функция C(m) для последовательности xk
C(m) = limn→∞
1/n ∑k=1,n
(xk - <x>)(xk+m - <x>) ,
<x> = limn→∞
1/n ∑k xk .
Если нам известна инвариантная мера для отображения, то
C(m) = limn→∞
1/n ∑k(xk - <x>)(f om(xk)
- <x>) = ∫(x - <x>)(f om(x) - <x>) dμ.
Например, для вырожденного отображения окружности
C(m) = 1/12 - δ(1 - δ) / 2 ,
где δ = mΔ (mod 1) и
корреляционная функция осциллирует с ростом m не затухая.
Для отображения пилы
C(m) = 2-m / 12 .
Т.о. перемешивание ведет к экспоненциальному затуханию корреляций
с ростом m.
Приложение: Перевод периодического
двоичного кода в рациональную дробь
Рассмотрим, например, десятичную периодическую дробь
0.(3) = 0.333... = 3 (10 -1 + 10 -2
+ 10 -3 + ...) = 3/[10(1 - 1/10)] = 3/9 = 1/3
(мы использовали формулу для суммы членов геометрической прогрессии).
Аналогично периодическую двоичную дробь представим в виде отношения
0.(101) = 1012 / 1112 = 5/7 (нижний
индекс 2 указывает на двоичную систему счисления).
Содержание
«Введение
»Динамика отображения тент
изменено 1 янв 2014
 Примеры: На Fig.4 показана вторая итерация отображения пилы и две точки
орбиты с периодом 2, полученные из символической последовательности
σ = (01) (см. Приложение)
Примеры: На Fig.4 показана вторая итерация отображения пилы и две точки
орбиты с периодом 2, полученные из символической последовательности
σ = (01) (см. Приложение)
 На Fig.1 приведено отображение зуб пилы
На Fig.1 приведено отображение зуб пилы
 Можно предположить, что хаос (и перемешивание траекторий) возникает из-за
разрыва отображения зуб пилы при x = 1/2. Однако подобное хаотическое
поведение наблюдается у непрерывного отображения "тент" (см. Fig.2 ниже)
и у совершенно гладкого квадратичного отображения.
Для отображения тент правила перевода символической последовательности
в двоичный код сложнее, чем для отображения пилы (см.
Динамика отображения тент на следующей странице).
Однако, существует простой трюк, позволяющий строить хаотические
последовательности для необратимых отображений.
Как видно из рисунка, при заданом xn всегда можно
выбрать предшествующее значение xn-1 лежащим в левом
или в правом интервале.
Поэтому итерируя обратное отображение легко построить орбиту для любой
символической последовательности (в том числе и хаотической).
Можно предположить, что хаос (и перемешивание траекторий) возникает из-за
разрыва отображения зуб пилы при x = 1/2. Однако подобное хаотическое
поведение наблюдается у непрерывного отображения "тент" (см. Fig.2 ниже)
и у совершенно гладкого квадратичного отображения.
Для отображения тент правила перевода символической последовательности
в двоичный код сложнее, чем для отображения пилы (см.
Динамика отображения тент на следующей странице).
Однако, существует простой трюк, позволяющий строить хаотические
последовательности для необратимых отображений.
Как видно из рисунка, при заданом xn всегда можно
выбрать предшествующее значение xn-1 лежащим в левом
или в правом интервале.
Поэтому итерируя обратное отображение легко построить орбиту для любой
символической последовательности (в том числе и хаотической).
 В общем случае для произвольного отображения разрешены не любые
σ-последовательности. Так для несимметричной пилы (слева) в правый
интервал можно попасть только из левого, поэтому комбинации 11 запрещены.
В общем случае для произвольного отображения разрешены не любые
σ-последовательности. Так для несимметричной пилы (слева) в правый
интервал можно попасть только из левого, поэтому комбинации 11 запрещены.