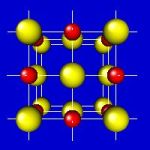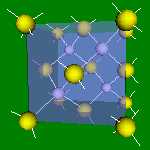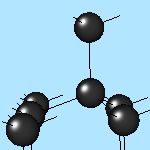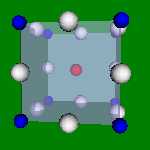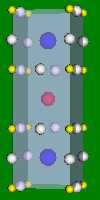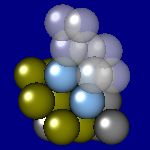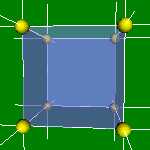
4x4x4 and 6x6x6 cells lattices.
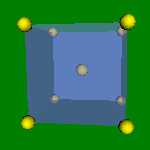
2x2x2 and 4x4x4 cells lattices. α-Fe, Na, K, β-Ti have this structure. The Wigner-Zeitz cell for the BCC lattice is truncated octahedron.
2x2x2 and 4x4x4 lattices. Cu, Au, Ag, Al, Pt, Pd have this structure. The Wigner-Zeitz cell for the FCC lattice is rhombic dodecahedron.