g1(c) = fc(0) = c = 0,
c1 [1 на рисунке ниже] = 0,
g2(c) = fco2(0) =
c2 + c = c (c + 1) = 0,
c1 = 0, c2 [2] = -1,
g3(c) = fco3(0) =
(c2 + c)2 + c =
c (c3 + 2c2 + c + 1) = 0,
c1 = 0, c2 [3a] = -1.75488,
c3 [3b] = c4* = -0.122561 + 0.744862i,
g4(c) = fco4(0) = 0,
c1 = 0, c2 = -1,
c3 [4a] = -1.9408, c4 [4b] = -1.3107,
c5 [4c] = c6* = -0.15652 + 1.03225i,
c7 [4d] = c8* = 0.282271 + 0.530061i.
Препериодические точки в множестве Мандельброта
Точка Mk,n в M препериодическая (Misiurewicz point) с периодом n, если ее критическая точка становится периодической с периодом n через k шагов. Препериодические точки Mk,n являются корнями уравненияfcok(0) = fco(k+n)(0) или gk(c) = gk+n (c).
Неподвижная точка z∗ = 1/2 ∓ (1/4 - c)½ (т.е. орбита с периодом 1) имеет мультипликатор λ∗ = 2z∗ = 1 ∓ (1-4c)½. Поэтому мультипликатор препериодической точки Mk,1 равен
λ∗ = 1/2 - (1/4 - Mk,1 )½.
Знак плюс соответствует единственной точке M2,1 = -2 (кончик антенны множества Мандельброта или точка кризиса) с мультипликатором λ = 4. Мультипликатор орбиты с периодом 2 равен λ2 = 4(c + 1) поэтому для Mk,2 получим
λ2 = 4(Mk,2 + 1).
Например критические орбиты M2,1 = -2 и M2,2 = i
(0, -2, 2, 2,...) и (0, i, i-1, -i, i-1, -i...)
соответственно. Обе орбиты неустойчивые с мультипликаторами
λ(-2) = 4 и λ(i) = 4(1 + i)
модули которых больше 1. Препериодические точки лежат на границе M. Ниже приведены некоторые препериодические точки с периодом 1.
| num | k | c | |λ| | Arg(λ)o |
| 1 | 2 | -2 | 4 | 0 |
| 2 | 3 | -1.54369 | 1.67857 | 180 |
| 3 | 3 | -0.22816+1.11514i | 3.08738 | -23.126 |
| 4 | 4 | -1.89291 | 1.92774 | 180 |
| 5 | 4 | -1.29636+0.44185i | 3.52939 | -5.7209 |
| 6 | 4 | -0.10110+0.95629i | 1.32833 | 119.553 |
| 7 | 4 | 0.34391+0.70062i | 2.45805 | -30.988 |
Вещественные препериодические точки
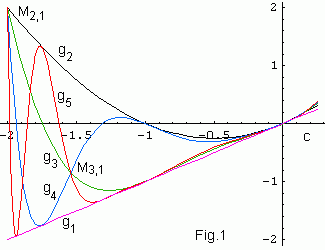 Для вещественных c полиномы g1,2,...,5(c)
показаны на Fig.1. Вещественные периодические точки являются корнями
этих полиномов. Пересечение двух кривых gk(c) =
gk+n(c) соответствует препериодической точке
Mk,n (показаны M2,1 и
M3,1). Fig.1 позволяет визуально определить
периодические и препериодические точки.
Для вещественных c полиномы g1,2,...,5(c)
показаны на Fig.1. Вещественные периодические точки являются корнями
этих полиномов. Пересечение двух кривых gk(c) =
gk+n(c) соответствует препериодической точке
Mk,n (показаны M2,1 и
M3,1). Fig.1 позволяет визуально определить
периодические и препериодические точки.
Содержание «Волосатые карлики »Точки Мисюревича и самоподобие множества Мандельброта
updated 29 ноября 2013