Бифуркации квадратичного отображения
За динамикой вещественного квадратичного отображения удобно следить
по бифуркационной диаграмме (налево внизу).
Будем строить итерации fc: x1 = 0 →
x2 → x3 → ...→ xMaxIt для
вещественных c на плоскости (x, c). Цвета (от синего к красному)
показывают, как часто орбита попадает в данную точку.
(переходный процесс показывает, как быстро итерации сходятся).
Вы можете также проследить за орбитой точки x = 0 при
соответствующем значении c на итерационной диаграмме справа.
Управление: Щелкните мышкой, чтобы растянуть бифуркационную
диаграмму в 2 раза. Щелкните мышкой с <Ctrl> чтобы
сжать картинку. Держите <Shift>,
чтобы растянуть изображение только в c (вертикальном) направлении.
MaxIt = 2000. Координаты центра изображения x,c и
Δx,Δc
отображаются в текстовом поле. Синяя вертикальная линия проходит через
начальную точку x = 0.
Верхняя часть диаграммы начинается с
касательной бифуркации при
c = 1/4. При -3/4 ≤ c ≤ 1/4 существует
единственная неподвижная притягивающая точка.
Рядом с c = -3/4 видна точка ветвления
бифуркации удвоения периода,
после чего неподвижная точка теряет
устойчивость и появляется притягивающая орбита с периодом 2.
Далее после новой бифуркации удвоения
периода возникает орбита с периодом 4 и т.д.
Каскад бифуркаций удвоения периода заканчивается при c = -1.401
после чего возникает область хаотической динамики,
которая заканчивается кризисом при c = -2.
В области хаотической динамики видны узкие горизонтальные белые полосы
окон регулярнойой динамики. Самая большая полоса внизу
соответствует окну с периодом 3.
В окне справа для сравнения приведено множеством Мандельброта (повернуто на
90o).
Распределение каустик на бифуркационной диаграмме
 Fig.1 поясняет, что каустики в распределении точек хаотических орбит
генерируются экстремумами отображения. Поэтому особенности (выделяемые красным
цветом) на диаграмме появляются на образах критической точки
fc on(0). Обозначая gn(c) =
fcon(0), получим
Fig.1 поясняет, что каустики в распределении точек хаотических орбит
генерируются экстремумами отображения. Поэтому особенности (выделяемые красным
цветом) на диаграмме появляются на образах критической точки
fc on(0). Обозначая gn(c) =
fcon(0), получим
go(c) = 0, g1(c) = c,
g2(c) = c2 + c, ...
Кривые g0,1,...,6(c) показаны на Fig.2.
Отметим, что аттрактор квадратичного отображения заключен между
кривыми g1(c) и g2(c).
Точка пересечения каустики с вертикальной прямой x = 0 на диаграмме
соответствует окну периодической динамики.
Содержание
«Итерации квадратичного отображения
»Итерации на комплексной плоскости
изменено 9 дек 2013
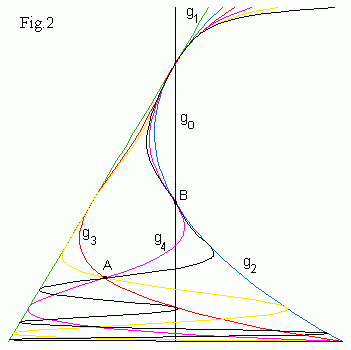
 Fig.1 поясняет, что каустики в распределении точек хаотических орбит
генерируются экстремумами отображения. Поэтому особенности (выделяемые красным
цветом) на диаграмме появляются на образах критической точки
fc on(0). Обозначая gn(c) =
fcon(0), получим
Fig.1 поясняет, что каустики в распределении точек хаотических орбит
генерируются экстремумами отображения. Поэтому особенности (выделяемые красным
цветом) на диаграмме появляются на образах критической точки
fc on(0). Обозначая gn(c) =
fcon(0), получим
