

| Однако, как следует из рисунка, существуют также "перекрученные" n раз решения φ(x) = 2πn x/L которым соответствуют локальные минимумы с энергией En ~ n2. |
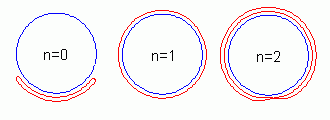
| Топологически не эквивалентные отображения Sx1 → Sn1 отличаются топологическим зарядом Q (или степенью отображения) который определяет сколько раз окружность Sx1 "наматывается" на Sn1. |

|
Чтобы вычислить Q можно проинтегрировать по всей цепочке
изменение угла dφ(x) между близкими векторами s(x) и
s(x+dx)
Q = 1/2π ∫ φ'(x) dx = Δφ/2π . |
|
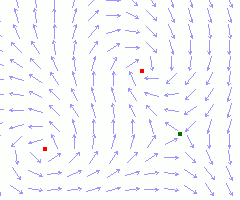
ВихриТопологические "дефекты" на плоскости появляются, если мы окружим некоторую область контуром на котором циркуляция φ отлична от нуля. Тогда внутри этого контура обязательно будет существоать вихрь. В трехмерном пространстве на такой контур нужно натянуть поверхность и тогда ее будет обязательно пересекать вихревая линяя. |

|

Для "непрерывной" XY-цепочку с Q ≠ 0 невозможно гладко перевести все синие стрелки вверх вращая спины в плоскости рисунка. Однако это можно сделать вращая стрелки вокруг оси x (в пространстве), т.е. для модели Гейзенберга. Поэтому у Гейзенберговского кольца нет топологических возбуждений. Это утверждение эквивалентно тому, что любое отображение окружности на сферу (т.е. призвольный замкнутый контур на ней) всегда можно стянуть в точку. |