

| Чтобы уменьшить полную энергию спинам выгодно соорентироваться вдоль магнитного поля. Поэтому основному минимуму соответствуют спины направленные вдоль поля. |
|
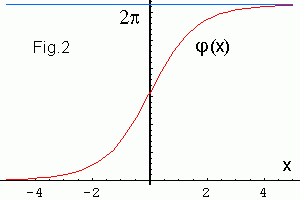
Уравнение для одномерной цепочки спинов в магнитном поле (*) совпадеает с
уравнением Ньютона для тела движущегося в потенциале cos x - 1 .
Нас интересует решение, которое выходит из неустойчивого положения равновесия
φ=0 и идет в следующий максимум потенциала φ=2π
(см. например [1])
φ(x) = 4 arctg(exp x) В отсутствии магнитного поля фаза φ линейно зависела от x. При включении поля фаза быстро меняется только в локальной области, ширина которой определяется величиной поля. С ростон h ширина кинка уменьшается. |

|
|
[1] Раджараман Р. Солитоны и инстантоны в квантовой теории поля (1985 г.)