
|

|
| Fig. a | Fig. b |
In applying Gauss's Law to find the electric field for a single point charge q, we used a spherical Gaussian surface (Fig. a)

|

|
| Fig. a | Fig. b |
Can we use other Gaussian surfaces to obtain the electric field at the same point P? For example, a cubic Gaussian surface as shown in Figure b? A little thought will convince us that this choice of a Gaussian surface will not enable us to calculate the electric field as easily as the spherical Gaussian surface. The statement of Gauss's Law
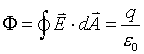
is still true for the cubic Gaussian surface, but there is no easy
way to untangle the electric field  from the integral. This is
because
from the integral. This is
because  is different at each
point on the cubic surface, both in magnitude and direction.
is different at each
point on the cubic surface, both in magnitude and direction.
Compare this to the situation in Figure a, where the electric field
vector  is directed radially
outward and has the same magnitude at every point on the spherical
Gaussian surface. Therefore, since the magnitude of the electric field
was a constant over the surface, we were allowed to take the electric
field out of the integral,
is directed radially
outward and has the same magnitude at every point on the spherical
Gaussian surface. Therefore, since the magnitude of the electric field
was a constant over the surface, we were allowed to take the electric
field out of the integral,
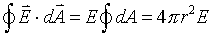
and
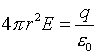
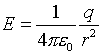
This illustrates an important point: that symmetry (in our example, spherical symmetry) plays a key role in applying Gauss's Law to calculate the electric field.
Go on to see an application of Gauss's Law, and then to try your hand at a practice problem.