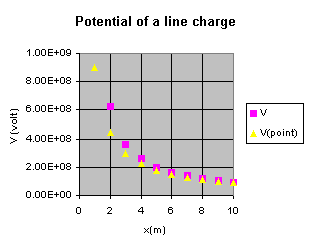
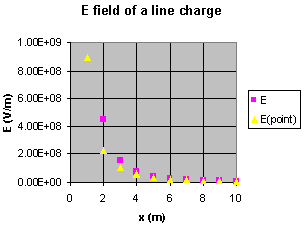
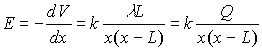Now we want to calculate the electrostatic potential due to a continuous charge distribution, and from that the electric field. As an example, consider a rod in which total charge Q is uniformly distributed over its length L. We will first consider the case of axial points - those points which lie along the same line as the charge.
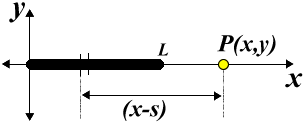
To calculate the potential at point P at distance x from the origin, we first find dV, the potential due to a small charge element within a segment ds, and all such contributions over the entire length L.
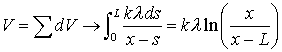
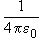 = 9
x 109 N m2/C2 and l
= linear charge density = Q/L.
= 9
x 109 N m2/C2 and l
= linear charge density = Q/L.