Квазипериодическая динамика и отображение окружности
В многомерных динамических системах с непрерывным временем
могут возникать колебания с несколькими
частотами. Их отношение зависит от параметров системы и если оно
иррационально, то возникает квазипериодическое движение.
При отношении частот близком к рациональному в нелинейных системах эти
колебания взаимодействуют обнаруживая тенденцию к взаимной
синхронизации (mode locking) и возникновению периодических режимов.
Квазипериодическая орбита с частотами ω1 и
ω2 располагается на торе. В сечении тора плоскостью
перпендикулярной его главной оси получается замкнутая кривая, точки
которой можно параметризовать угловой координатой
0 ≤ θ < 2π.
Траектория, выходящая из точки θn снова
пересекает плоскость в точке θn+1
и задает отображение Пуанкаре
θn+1 =
θn + f(θn ).
Отображение окружности
Если в f(θ) ограничиться нулевой и первой гармониками,
то мы получаем нелинейное отображение окружности
θn+1 = θn +
Δ + k sin θn (mod 2π).
Траектории отображения удобно характеризовать числом вращения
(winding number), которое определяется, как среднее приращение θ
за одно отображение, измеренное в долях полного угла
w = limn→∞ (θn -
θo)/2πn
при подсчете w угол θ не приводится к интервалу
(0,2π).
При k = 0 отображение сводится к повороту окружности на
постоянный угол Δ, число вращения w = Δ/2π и
ни при каких Δ ≠ 0 неподвижных точек нет.
Рациональным значениям Δ/2π = p/q с целыми
p и q соответствуют периодические орбиты с "частотой"
(p, q). Такая орбита оборачивается вокруг окружности p раз за
q итераций. Иррациональным Δ/2π соответствуют
всюду плотные на окружности квазипериодические траектории.
При k < 1 отображение монотоно и обратимо.
В этой области также возможны периодические и квазипериодические орбиты
с иррациональными числами вращения и нулевым ляпуновским показателем.
Идущие вниз к k = 0 и θ/2π = p/q
языки Арнольда соответствуют резонансным периодическим орбитам
(p, q) (синхронизация нелинейных колебаний).
Мера областей значений Δ соответствующих квазипериодической
динамике (они окрашены черным цветом) убывает до нуля при k → 1.
Бифуркационная (изопериодическая) диаграмма на
плоскости параметров (Δ/2π, k/2π).
Щелкните мышкой, чтобы определить период n в указанной точке.
Щелкните мышкой + <Alt>(<Ctrl>) чтобы увеличить
(уменьшить) изображение в 2 раза.
В области k > 1 отображение немонотонно, не является
взаимно-однозначным и у него могут появляються хаотические траектории
с положительным ляпуновским показателем. Внутри области
хаотической динамики снова видны окна регулярной динамики
(ласточки Милнора).
Периодические орбиты отображения
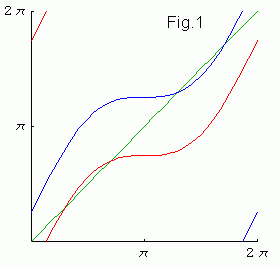 Как следует из Fig.1 при k отличном от нуля у отображения могут
появиться притягивающая и отталкивающая неподвижные точки. Они определяются
уравнением
Как следует из Fig.1 при k отличном от нуля у отображения могут
появиться притягивающая и отталкивающая неподвижные точки. Они определяются
уравнением
θo = θo + Δ +
k sin θo
откуда следует
-sin θo = Δ / k ≤ 1.
Т.о. в области k ≥ Δ существует устойчивая орбита 0/1
(соответствует первому пересечению синей кривой с диагональю на рисунке).
С ростом k она теряет устойчивость из-за бифуркации удвоения
периода. В точке бифуркации производная отображения λ =
1 + k cos θo = -1. Легко убедиться, что это происходит
на гиперболе k2 = Δ2 + 4.
Устойчивая орбита 1/1 (соответствует пересечению красной кривой с
диагональю) определяется уравнением
θo + 2π = θo +
Δ + k sin θo.
Она существует при условии k ≥ 2π - Δ.
Для области полуцелого резонанса 1/2 раскладывая вторую итерацию
отображения по малым k можно получить приближенно [1]
π - k2/4 < Δ <
π + k2/4,
что хорошо согласуется с приведенной выше картинкой.
[1] Елютин П.В.
НЕЛИНЕЙНАЯ ДИНАМИКА
Лекция 14
Содержание
«"Ласточки" и "креветки"
»Отображение пекаря
изменено 19 июня 2006
 Как следует из Fig.1 при k отличном от нуля у отображения могут
появиться притягивающая и отталкивающая неподвижные точки. Они определяются
уравнением
Как следует из Fig.1 при k отличном от нуля у отображения могут
появиться притягивающая и отталкивающая неподвижные точки. Они определяются
уравнением