Двумерная бифуркационная диаграмма. "Ласточки" и "креветки"
Напомним, что главной особенностью области регулярной динамики квадратичного
отображения, окруженной хаотической областью, является существование параметра
c при котором отображение имеет сверхустойчивый цикл периода n
(включающий критическую точку отображения). В этой области итерации
f on(x) хорошо апроксимируются квадратичным отображением.
При наличии двух параметров, орбита будет сверхустойчивой вдоль некоторой
кривой в пространстве параметров. В перперндикулярном к этой
кривой направлении бифуркации будут повторять бифуркации квадратичного
отображения.
Однако, если у отображения более чем одна критическая точка, то в точке
пересечения двух кривых сверхустойчивости орбита становится
дважды-сверхустойчивой. Рядом с этой точкой она хорошо апроксимируется
композицией двух квадратичных отображений
y' = x2 + c1 ,
x' = y2 + c2 или
x' = (x2 + c1)2 +
c2 ,
и линейной заменой координат (A,B) сводится к каноническому
биквадратичному отображению [1,2].
Здесь на плоскости (A,B) вы видите "ласточку" (или "креветку")
соответствующую окну регулярной динамики с периодом 3.
Управление
Щелкните мышкой, чтобы определить период орбиты n в выбранной точке.
Щелкните мышкой + <Alt>(<Ctrl>) чтобы увеличить
(уменьшить) изображение в 2 раза.
Держите <Shift> чтобы изменить масштаб в 4 раза.
Биквадратичное отображение и ласточка Милнора
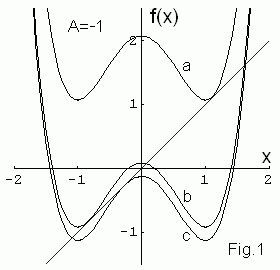
Как видно из Fig.1, у вещественного биквадратичного отображения,
зависящего от двух вещественных параметров (A,B)
xn+1 = f(xn ) =
(xn2 + A)2 + B
может быть одна или две устойчивые неподвижные точки. Каждая из них
притягивает к себе ближайшие критические точки
x0 = 0 или
x1,2 = ±(-A)1/2
при A < 0
(очевидно, что орбиты, начинающиеся в x1 и
x2 совпадают). Пусть A = -1, тогда при B ~ 1
происходит первая касательная бифуркация в которой рождаются устойчивая и
неустойчивая неподвижные точки (самая верхняя кривая - a на рисунке).
При уменьшении B происходит вторая касательная бифуркация и у
отображения появляется еще одна притягивающая точка (кривая - b).
Наконец, далее происходит
обратная касательная бифуркация при которой устойчивая точка сливается с
неустойчивой и они обе исчезают (самая нижняя кривая - c).
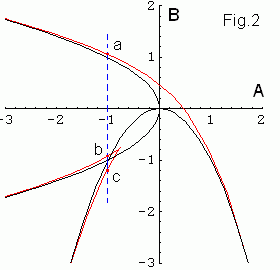
На Fig.2 внизу на плоскость параметров (A,B) построены три красные
кривые на которых происходят эти касательные бифуркации.
Там же построена парабола B = -A2 на которой критическая
точка x0 совпадает с неподвижной. На параболе
A = -B2 неподвижна x1.
Эти кривые образуют силуэт "ласточки Милнора" [1].
"Охотник за креветками"
Для построения бифуркационной диаграммы
при каждом значении (A,B) отображение итерируется 500 раз
(начиная с одной из критических точек), после чего определяется период
полученной траектории.
Если итерации выходят на периодическую орбиту, тоочка окрашивается в
соответствии с периодом. Если период больше 64, то строится черная
точка, чтобы улучшить видимость маленьких "креветок". Заметим, что
из-за медленной сходимости итераций в областях бифуркаций на картинке
могут появляться нехаотические черные
полосы между областями с разными периодами.
[1] J.Milnor "Remarks on iterated cubic maps"
Exp.Math. 1 (1992), 5.
[2] B.R.Hunt, J.A.C.Gallas, C.Grebogi, J.A.Yorke, and
H.Kocak Bifurcation
Rigidity
Physica D 129 (1999), 35.
[3] Canonical Quartic Map
Содержание
«"переходный" хаос
»Отображение окружности
изменено 28 июля 2015

