Отображение пекаря
Отбрасывание старшего символа последовательности при сдвиге Бернулли
делает отображение пилы необратимым. Чтобы
получить обратимое отображение достаточно взять бесконечную в обе стороны
последовательность бинарных символов
... S-2, S-1, S0 ;
S1, S2, ...
которую теперь можно двигать влево и вправо относительно точки с запятой.
Сопоставим этой последовательности два вещественных числа
x = 0. S1 S2 S3 ...
y = 0. S0 S-1 S-2 ...
Нетрудно проверить, что при сдвиге символической последовательности
влево получаются новые значения
x' = 2x mod 1
y' = 1/2 (y + [2x])
где [x] означает целую часть x.
Это преобразование единичного квадрата в себя называется
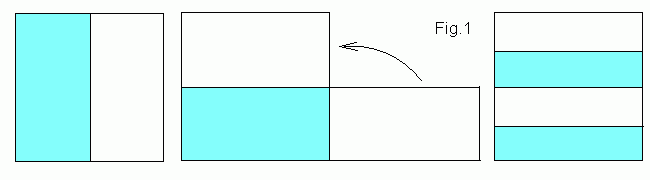
отображением пекаря (baker's map). Преобразование состоит из
однородного сжатия квадрата в 2 раза в вертикальном направлении и
растяжения в горизонтальном. Далее правую половину следует отрезать и
положить на левую. Действие двух первых его итераций показано на Fig.1.
Неустойчивые периодические орбиты
Как и для отображения пилы по символической последовательности легко
находятся периодические орбиты отображения. Так
символическим последовательностям состоящим из 0 и 1
соответствуют неподвижные точки (x, y) = (0, 0) и (1, 1).
Периодической последовательности (10) соответствует орбита из двух точек
(1/3, 2/3) и (2/3, 1/3). Наконец, из последовательности
...001;001... получаем орбиту (1/7, 4/7), (2/7, 2/7), (4/7, 1/7),
а из ...011;011... орбиту (3/7, 6/7), (6/7, 3/7), (5/7, 5/7)
с периодом 3.
Любые x и y можно сколь угодно точно аппроксимировать
двоичными последовательностями 0.Xo...Xn и
0.Yo...Ym, где n и m достаточно
велики. Поэтому периодическая последовательность
(Ym ...Yo Xo ...Xn ) пройдет
сколь угодно близко к любой точке квадрата. Т.е. неустойчивые периодические
орбиты образуют всюду плотное множество.
Перемешивание и хаотические траектории
Т.к. отображение состоит из растяжения вдоль оси x и сжатия вдоль
y, то близкие траектории экспоненциально расходятся в горизонтальном
направлении и сближаются в вертикальном. Как и для отображения пилы, из
случайной символической последовательности строится хаотическая траектория,
которая проходит сколь угодно близко к каждой точке квадрата (эргодичность).
Очевидно, что под действием отображения любая выбранная область будет
превращаться в совкупность узких горизонтальных полос, которая
через некоторое число итераций равномерно покроет единичный квадрат
(перемешивание). Преобразование обратимо, при итерациях в обратном направлении
любая область будет разбиваться на узкие вертикальные полоски и также
перемешается по всему квадрату.
Содержание
«Отображение окружности
»Подкова Смейла и странные репеллеры
изменено 29 ноября 2005
