Переход к хаосу через перемежаемость
 Чередование фаз регулярной и хаотической динамики называется
перемежаемостью. Перемежаемость наблюдается в области параметров
рядом с касательной бифуркацией (в верххней части
окна периодического движения на бифуркационной диаграмме).
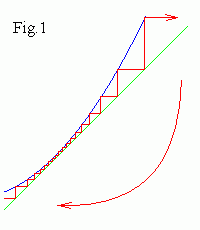
На Fig.1. показано, что при увеличении c,
когда устойчивая неподвижная точка сливается с неустойчивой и обе исчезают,
орбита медленно проходит через узкий "корридор" и расходится.
После этой регулярной фазы орбита уходит в область с хаотической динамикой,
а затем снова возвращается в корридор (реинжекция).
Первые два рисунка ниже демонстрируют, как медленно расходится орбита точки
x = 0 при c близком к бифуркационному значению
c* = -1.75 .
Хаотические орбиты с положительными показателями Ляпунова показаны ниже.
Можно показать [1], что длительность регулярной фазы пропорциональна
(c* - c)-1/2. Т.е. она увеличивается в 2 раза
если уменьшить (c* - c) в 4 раза, в соответствии с
приведенными рисунками.
Чередование фаз регулярной и хаотической динамики называется
перемежаемостью. Перемежаемость наблюдается в области параметров
рядом с касательной бифуркацией (в верххней части
окна периодического движения на бифуркационной диаграмме).
На Fig.1. показано, что при увеличении c,
когда устойчивая неподвижная точка сливается с неустойчивой и обе исчезают,
орбита медленно проходит через узкий "корридор" и расходится.
После этой регулярной фазы орбита уходит в область с хаотической динамикой,
а затем снова возвращается в корридор (реинжекция).
Первые два рисунка ниже демонстрируют, как медленно расходится орбита точки
x = 0 при c близком к бифуркационному значению
c* = -1.75 .
Хаотические орбиты с положительными показателями Ляпунова показаны ниже.
Можно показать [1], что длительность регулярной фазы пропорциональна
(c* - c)-1/2. Т.е. она увеличивается в 2 раза
если уменьшить (c* - c) в 4 раза, в соответствии с
приведенными рисунками.
Перемежаемость на комплексной плоскости
На комплексной плоскости касательная бифуркация происходит рядом с
острием кардиоиды каждого М-карлика. Для карлика с периодом 3 (налево)
перемежающиеся траектории находятся на луче
Im(c) = 0, Re(c) > -1.75. Карлики m7, m8 и
m50 соответствуют орбитам с периодами 7, 8, 50
(синхронизация). Периодические орбиты образуют плотное множество на этом луче.
Ниже показана периодическая орбита, соответствующая карлику m50.
[1] J.Hanssen, W.Wilcox
Lyapunov Exponents for the
Intermittent Transition to Chaos
Содержание
«Переход к хаосу через удвоение периода
»Канторовы структуры
изменено 6 июня 2006
 Чередование фаз регулярной и хаотической динамики называется
перемежаемостью. Перемежаемость наблюдается в области параметров
рядом с касательной бифуркацией (в верххней части
окна периодического движения на бифуркационной диаграмме).
На Fig.1. показано, что при увеличении c,
когда устойчивая неподвижная точка сливается с неустойчивой и обе исчезают,
орбита медленно проходит через узкий "корридор" и расходится.
После этой регулярной фазы орбита уходит в область с хаотической динамикой,
а затем снова возвращается в корридор (реинжекция).
Первые два рисунка ниже демонстрируют, как медленно расходится орбита точки
x = 0 при c близком к бифуркационному значению
c* = -1.75 .
Чередование фаз регулярной и хаотической динамики называется
перемежаемостью. Перемежаемость наблюдается в области параметров
рядом с касательной бифуркацией (в верххней части
окна периодического движения на бифуркационной диаграмме).
На Fig.1. показано, что при увеличении c,
когда устойчивая неподвижная точка сливается с неустойчивой и обе исчезают,
орбита медленно проходит через узкий "корридор" и расходится.
После этой регулярной фазы орбита уходит в область с хаотической динамикой,
а затем снова возвращается в корридор (реинжекция).
Первые два рисунка ниже демонстрируют, как медленно расходится орбита точки
x = 0 при c близком к бифуркационному значению
c* = -1.75 .