Канторовы структуры
Канторов репеллер
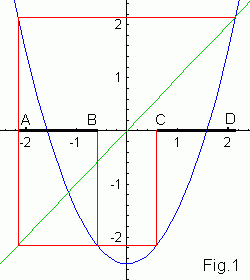
Как видно из рисунка, при c < -2 интервал (BC) отображается
за пределы инвариантного интервала Ic и при итерациях
его точки уходят на бесконечность. Два интервала [AB] и [BC]
отображаются на Ic. Поэтому, так же как и для
отображения тент (последовательным удалением
центральной части отрезков), у квадратичного отображения возникает
обладающий нулевой мерой канторов репеллер.
Странный репеллер и регулярная динамика
Однако подобные структуры возникают и, например, при
c = -1.7542 (соответствующем окну регулярной динамики).
Почти для всех x из интервала Ic
траектория притягивается к орбите с периодом-3 (эти точки лежат внутри
окружностей). Оставшиеся (после удаления этих окружностей) точки снова образуют
классическое множество Кантора - странный репеллер с нулевой мерой.
Как мы уже знаем, устойчивый и неустойчивый циклы квадратичного
отображения с периодом p рождаются при касательной бифуркации
f op(x). При дальнейшем уменьшении параметра c
притягивающий цикл теряет устойчивось и рождается новый устойчивый цикл
с удвоенным периодом. Неустойчивые циклы уже никогда не исчезают.
Т.о. после завершения каскада бифуркаций удвоения периода у квадратичного
отображения возникает бесконечное множество неустойчивых периодических орбит.
Основная дихотомия для квадратичного отображения
Почти для каждого c в [-2, 1/4],
квадратичное отображение fc : x →
x 2 + c или регулярное или стохастическое [1]
Для квадратичных отображений множество значений
параметра c с хаотическим аттрактором имеет положительную меру Лебега,
а притягивающие периодические орбиты плотны в этом интервале. Т.е. между
любыми двумя хаотическими параметрами c всегда существует периодический
интервал.
Это можно мотивировать следующим образом. Для c соответствующего
хаотической динамике рассмотрим критическую орбиту (выходящую из x = 0).
Обычно через некоторое количество итераций эта орбита вернется достаточно
близко к начальной точке. После чего ее можно будет "подогнать" к
x = 0 малым изменением параметра c, получив т.о. сверхустойчивый
цикл.
"Толстое" множество Кантора
Если в канторовом процессе выбросить центральную 1/3 часть интервала,
затем центральную 1/9 у двух оставшихся отрезков, потом 1/27
и т.д., то полученное множество будет топологически эквивалентно классическому.
Но т.к. "дыры" быстро уменьшаются в размерах, то "толстое" множество Кантора
обладает положительной мерой Лебега и фрактальной размерностью 1.
Так на интервале -2 ≤ c ≤ 1/4, области с хаотической динамикой
обладают положительной мерой Лебега и образуют толстое множество Кантора.
Ниже можно убедиться, что области регулярной динамики (черные М-карлики)
плотны вдоль вещественной оси на комплексной плоскости.
[1] Mikhail Lyubich
The
Quadratic Family as a Qualitatively Solvable Model of Chaos
Notices of the AMS, 47, 1042-1052 (2000)
Содержание
«Переход к хаосу через перемежаемость
»"Переходный" хаос
изменено 5 янв 2014
