Нелинейный резонанс
На этой страничке мотивируется универсальность динамики стандартного
отображения. Сначала мы напоминаем основные свойства нелинейного маятника.
Далее поясняется возникновение резонансных слагаемых в теории возмущений
и вводится понятие нелинейного резонанса. Лучше это прочитать в учебнике.
Без особого вреда вы можете перейти прямо к
стандартному отображению.
Нелинейный маятник
Гамильтониан и уравнения движения нелинейного маятника
H(p,x) = p2/2 + V(x)
= p2/2 + Vocos x = E = const
dx/dt = ∂ H/∂ p = p ,
dp/dt = -∂ H/∂ x = Vo sin x .
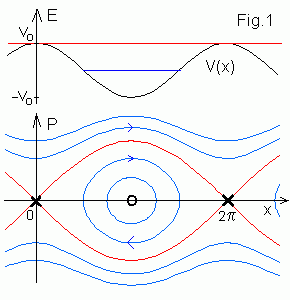 При -Vo < E < Vo частица осциллирует
между двумя точками поворота. На фазовой плоскости (x, p) орбита
вращается (синий овал) вокруг эллиптической неподвижной точки O
(положения равновести при x = π ).
При E > Vo частица проходит над максимумом
потенциала V(x) и уходит на бесконечность. Т.к. V(x)
периодично, то можно рассмотреть движение на цилиндре и соединить точки
0 и 2π. Красная сепаратриса (или гомоклиническая
орбита) при E = Vo разделяет эти две области.
Она выходит из одной гиперболической точки X (положения неустойчивого
равновесия в x = 2πn) и приходит в другую. Движение около
сепаратрисы очень чувствительно к возмущениям, т.к. даже малое возмущение
может перебросить частицу над барьером и изменить топологию орбиты.
Ширина гомоклинической орбиты
При -Vo < E < Vo частица осциллирует
между двумя точками поворота. На фазовой плоскости (x, p) орбита
вращается (синий овал) вокруг эллиптической неподвижной точки O
(положения равновести при x = π ).
При E > Vo частица проходит над максимумом
потенциала V(x) и уходит на бесконечность. Т.к. V(x)
периодично, то можно рассмотреть движение на цилиндре и соединить точки
0 и 2π. Красная сепаратриса (или гомоклиническая
орбита) при E = Vo разделяет эти две области.
Она выходит из одной гиперболической точки X (положения неустойчивого
равновесия в x = 2πn) и приходит в другую. Движение около
сепаратрисы очень чувствительно к возмущениям, т.к. даже малое возмущение
может перебросить частицу над барьером и изменить топологию орбиты.
Ширина гомоклинической орбиты
max Δp = 4 V o1/2.
Резонансы
В канонических переменных угол-действие (I, θ) гамильтониан
системы с одной степенью свободы H(I) зависит только от I и
уравнения движения
dI/dt =
-∂H(I)/∂θ = 0 , I = const ,
dθ/dt = ∂H(I)/∂I = ω(I) =
const .
При включении периодического возмущения V(I, θ, t) = V(I, θ, t + T)
H(I, θ, t) =
Ho(I) + εV(I, θ, t) = Ho(I) +
ε∑ n,m Vnm(I) einθ -
imΩt ,
dI/dt = -∂ H/∂ θ =
-iε∑ n,m nVnm(I) einθ -
imΩt , (*)
dθ/dt = ∂ H/∂ I .
где Ω = 2π /T. Для малых ε можно искать
решение в виде ряда
I = I o + εI 1 + ... ,
θ = θ o + εθ 1 + ... ,
I o = const,
θ o = ω(I o)t .
После подстановки I o, θ o
в (*) получим
dI 1/dt =
-i∑ n,m nVnm(I o)
exp[i(nω(I o) - mΩ)t] ,
I 1 =
-∑ n,m nVnm(I o)
/[nω(I o) - mΩ]
ei[nω(I o) - mΩ]t + const .
В резонансе nω(I) - mΩ = δnm ~ 0 ,
I 1 и θ 1 содержат расходящиеся
слагаемые с малыми знаменателями Vnm /δnm.
В нелинейных системах частота ω(I) зависит от I,
поэтому резонансы при некоторых I, n, m могут возникать на любой
частоте Ω.
Приближение одиночного резонанса.
Универсальный гамильтониан
Чтобы избежать расходимости для одиночного резонанса можно решить (*)
учитывая расходящееся слагаемые с nω - mΩ ~ 0
dI/dt = εnVnm
sin(nθ - mΩt + φ) ,
dθ/dt = ω(I) + ε dVnm/dI
cos(nθ - mΩt + φ) .
Соответствующий гамильтониан
H = Ho(I) + εVnm(I)
cos(ψ), ψ = nθ - mΩt + φ.
Для малых ΔI = I - Io
его можно привести к гамильтониану нелинейного маятника
H(ΔI, ψ) = nω' ΔI 2/2 +
nεV cos( ψ ) ,
ω' = dω/dI .
Т.о. независимо от ω(I), V(I) динамика около одиночного
резонанса приближенно описывается этим универсальным гамильтонианом.
Резонансные слагаемые приводят к появлению гомоклинических траекторий на
фазовой плоскости (ψ, ΔI) (подобных Fig.1) с шириной
max ΔI = 4 (εV/|ω'|)1/2 .
Нерезонансные слагаемые приводят к хаотической динамике около
гомоклинических траекторий. Чтобы увидеть это можно строить точки
траектории в моменты t = nT. Одним из примеров является стандартное
отображение. Ниже вы видите резонансы, инвариантные окружности и хаотические
области около гомоклинических траекторий.
Содержание
«Странный аттрактор Эно
»Стандартное отображение
изменено 19 мая 2006
 При -Vo < E < Vo частица осциллирует
между двумя точками поворота. На фазовой плоскости (x, p) орбита
вращается (синий овал) вокруг эллиптической неподвижной точки O
(положения равновести при x = π ).
При E > Vo частица проходит над максимумом
потенциала V(x) и уходит на бесконечность. Т.к. V(x)
периодично, то можно рассмотреть движение на цилиндре и соединить точки
0 и 2π. Красная сепаратриса (или гомоклиническая
орбита) при E = Vo разделяет эти две области.
Она выходит из одной гиперболической точки X (положения неустойчивого
равновесия в x = 2πn) и приходит в другую. Движение около
сепаратрисы очень чувствительно к возмущениям, т.к. даже малое возмущение
может перебросить частицу над барьером и изменить топологию орбиты.
Ширина гомоклинической орбиты
При -Vo < E < Vo частица осциллирует
между двумя точками поворота. На фазовой плоскости (x, p) орбита
вращается (синий овал) вокруг эллиптической неподвижной точки O
(положения равновести при x = π ).
При E > Vo частица проходит над максимумом
потенциала V(x) и уходит на бесконечность. Т.к. V(x)
периодично, то можно рассмотреть движение на цилиндре и соединить точки
0 и 2π. Красная сепаратриса (или гомоклиническая
орбита) при E = Vo разделяет эти две области.
Она выходит из одной гиперболической точки X (положения неустойчивого
равновесия в x = 2πn) и приходит в другую. Движение около
сепаратрисы очень чувствительно к возмущениям, т.к. даже малое возмущение
может перебросить частицу над барьером и изменить топологию орбиты.
Ширина гомоклинической орбиты