Subgraphs and Supergraphs
A subgraph of a graph
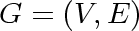 is a graph
is a graph
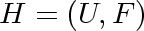 such that such that
 and and
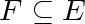 . .
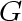 would then be a supergraph for would then be a supergraph for  . .
Example:
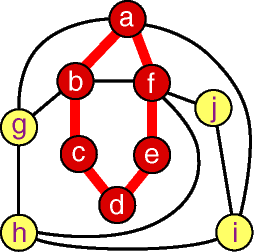 Figure 9: Subgraph and Supergraph
The cycle of length 6 (red vertices and edges) is a
subgraph of the whole graph. Notice that not all edges
connecting the shaded vertices belong to the subgraph.
The subgraph is a supergraph for the cycle. Figure 9: Subgraph and Supergraph
The cycle of length 6 (red vertices and edges) is a
subgraph of the whole graph. Notice that not all edges
connecting the shaded vertices belong to the subgraph.
The subgraph is a supergraph for the cycle.
|
 is an induced subgraph of is an induced subgraph of
 if all edges of if all edges of  connecting vertices in
connecting vertices in  belong to belong to  . .
Example:
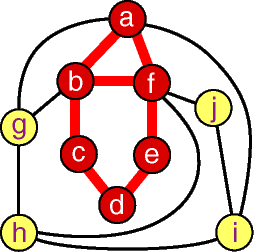 Figure 10: An Induced Subgraph
The six red vertices and seven red edges (a cycle with
a chord) form an induced subgraph of the whole
graph. All edges connecting the shaded vertices belong
to the subgraph. Figure 10: An Induced Subgraph
The six red vertices and seven red edges (a cycle with
a chord) form an induced subgraph of the whole
graph. All edges connecting the shaded vertices belong
to the subgraph.
|
A subgraph containing all vertices of the graph is called spanning.
| 


