Walks, Paths, Cycles
A walk from vertex 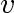 to a vertex to a vertex  is a sequence of alternating vertices and edges
is a sequence of alternating vertices and edges
 Equation
6
Equation
6
such that
-
 , ,
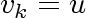 , and , and
-
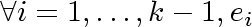 is incident with
is incident with 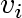 and and
 . .
A walk is called a path if it does not repeat any vertex.
A graph is called connected if, for any two vertices 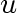 and
and  of the graph, there is a walk from of the graph, there is a walk from 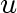 to to 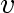 . .
A connected component is a maximal connected subgraph.
A subset  of vertices of a graph of vertices of a graph 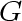 is a connected component if and only if: is a connected component if and only if:
-
For any two vertices in
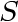 , there is a path connecting them. , there is a path connecting them.
-
Any vertex not in
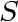 is not adjacent to any vertex in is not adjacent to any vertex in  . .
A closed walk is a walk whose first and last vertices are
the same.
A cycle is a closed walk which does not repeat any vertex,
except for the first and the last.
| 


