Edges and Vertices
Now that you understand what a graph is, let's define some
useful terms relative to the edges and vertices of a graph:
If an edge
 is an edge in a graph, then is an edge in a graph, then
-
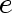 is said to be
incident with vertices is said to be
incident with vertices
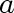 and and
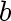 . .
-
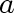 and and  are also said to be
incident with are also said to be
incident with 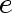 . .
-
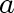 and and  are
adjacent to one another. are
adjacent to one another.
The degree of a vertex
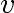 is the number of vertices
adjacent to is the number of vertices
adjacent to 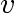 . (This equals
the number of edges incident with . (This equals
the number of edges incident with
 ). ).
Example:
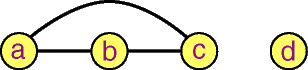 Figure 5: Degree
In this graph, vertices Figure 5: Degree
In this graph, vertices
 , ,
 , and , and
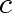 have degree 2, while
vertex have degree 2, while
vertex 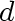 is an
isolated vertex (its degree is 0).
Notation: is an
isolated vertex (its degree is 0).
Notation:
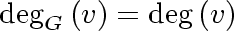 . .
|
An isolated vertex is a vertex of degree
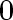 . In the example graph
above, . In the example graph
above,  is an isolated
vertex. is an isolated
vertex.
A graph is regular if the degrees of all
vertices are equal. A graph is
r-regular if
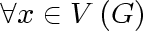 , ,
 . .
When are graphs the same?
A graph is fully defined by its vertex and edge sets.
However, the same graph can be drawn differently. Different
ways to represent the same graph are often considered
immaterial. This approach is captured by the definition of
isomorphic graphs:
| 


