Modeling it as a Graph Theory Problem
Modeling The Drilling Problem As A Graph Theory Problem
Now that we have covered the fundamentals of graph theory, let us return to the
drilling problem. In order to use what we have learned about graph theory, we will reformulate
the problem as a graph theory problem as shown below:
Recall the pattern that was to be drilled into the workpiece by the gang drill:
The Final Product:
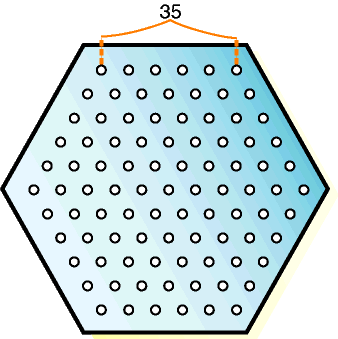 Figure 26: The Final Product
The pattern of holes that had to be drilled into the
workpiece with a gang drill. Figure 26: The Final Product
The pattern of holes that had to be drilled into the
workpiece with a gang drill.
|
The set of 91 points on the plane is viewed as a set of vertices in a graph 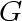 .
There are exactly 91 vertices. Each of them corresponds to a point;
different vertices correspond to different points. .
There are exactly 91 vertices. Each of them corresponds to a point;
different vertices correspond to different points.
The set of edges in the graph 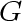 is the set of pairs of vertices
whose corresponding vertices are less than 35 units apart. is the set of pairs of vertices
whose corresponding vertices are less than 35 units apart.
Any set of points that can be drilled in one pass corresponds to
vertices in 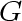 that form an independent set. that form an independent set.
The sequence of passes that would yield all points drilled corresponds
to a set of independent sets that cover the whole graph.
Such a set of independent sets is a vertex coloring of the graph.
|
Conclusion
The drilling problem is identical to the problem of coloring the graph  using the smallest possible number of colors.
Recall that this number is called the chromatic number of the graph.
using the smallest possible number of colors.
Recall that this number is called the chromatic number of the graph.
|
We have two objectives:
-
Construct a coloring of the graph; and
-
Prove that the number of colors used is minimum.
| 


